My cousin sent me this query from the dubious Quora:
“In the Book of Genesis, only 8 humans, Noah and his sons and their four wives, survived the Flood. How many people could a family of 8 procreate in, say, 500 years?”
Tag Archives: exponential growth
Coronavirus Mathematics
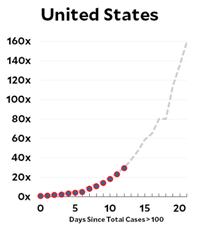Given the mathematical nature of this website I feel reluctantly impelled to address the coronavirus pandemic. The mathematics behind the spread of infection is basically the same exponential growth that I discussed in the “Math and Religion” post and has recently been explained by the ever-lucid Grant Sanderson at his 3Blue1Brown website.
What I wish to draw attention to is the series of posts on the coronavirus by Kevin Drum on his website at Mother Jones. I have collected his recent posts comparing the spread of the virus in various countries and added some mathematical commentary of my own, which is the content of this post.
But the bottom line seems to be that in virtually all the countries, including the US, the virus infection is spreading at the Italian rate of doubling every 4 days! The readers of this website are sufficiently numerate to realize the frightening import of that number. If that weren’t enough, Kevin provides additional posts on the results of the modeling at the Imperial College that are truly nerve-wracking for someone such as myself in the most vulnerable cohort. The only blessing so far seems to be that, for once, the children are spared.
At this time, I don’t have the stomach to keep updating the post as new numbers come in. That may change. I could address the catastrophe of having ignorance and incompetence at the helm of the national ship of state, but it is too depressing.
See the Coronavirus Mathematics
(Updates 3/17/2020, 3/21/2020, 4/17/2020, 9/20/2020, 10/1/2020) Continue reading
Exponential Yarn
Tanya Khovanova’s recent blog post “The Annoyance of Hyperbolic Surfaces” about crocheting a hyperbolic surface added to the numerous examples of such activity, usually from knitting. Somehow this post caught my attention, in particular about the exponential growth of each added row and the fact that the resulting “surface” had constant negative curvature. I explored the exponential growth in this article and saved the mathematical exploration of the constant negative curvature for a later essay. See Exponential Yarn.
Math and Religion
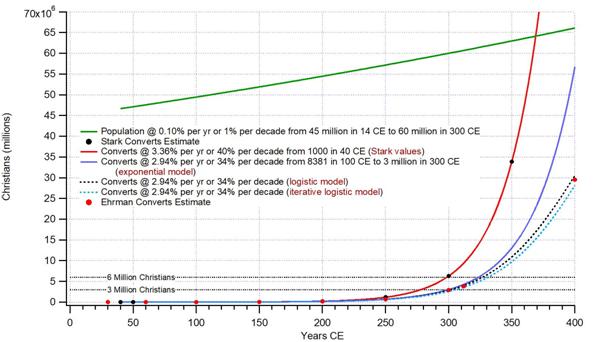This was a catchy, misleading title that I could not resist, since my essay is not about math vs. religion as one might expect from the title, but rather about math helping religion. Back in 2016 I was reading Dr. Bart D. Ehrman’s blog that he was writing in preparation for his eventual book, The Triumph of Christianity, in which he was considering Rodney Stark’s purely mathematical analysis of the growth of Christianity in the first three centuries. Neither Rodney Stark nor Bart Ehrman described explicitly the underlying mathematical models of exponential growth that they were using and exactly what was meant by a rate of growth. Given the natural audience for the subject, these omissions were not surprising. So I thought I would clarify the math and also offer some variations on the models, which eventually reflected the actual situation more faithfully. See Math and Religion.
Hossenfelder Stagnation Problem
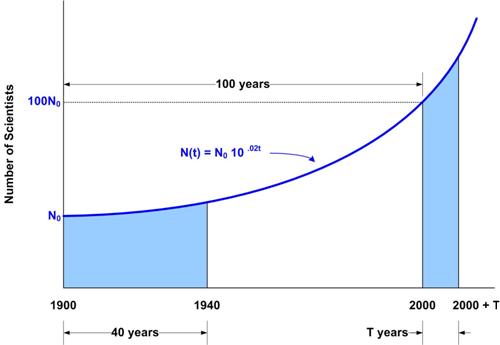Sabine Hossenfelder wrote an excellent blog posting about the growing awareness that outstanding scientific problems are not getting solved at the same rate as in the past. Her whole article is worth a read, as are all her postings, but this latest contained a mathematical statement that warranted justification. For scientists “How much working time starting today corresponds to, say, 40 years working time starting 100 years ago. Have a guess! Answer: About 14 months.” See Hossenfelder Stagnation Problem.
Ancestors Problem
In 2011 I wrote about an amusing article in the 9 September 1978 Washington Post in which the reporter, Henry Allen, began thinking about the number of ancestors he had 10 generations ago. He figured that each generation had 2 parents, so the 10th generation would have 2^10 or over a thousand members. At 25 years per generation he started imagining the expanding number of direct ancestors he had going back through history, achieving astronomical numbers, which did not seem reasonable. As reporters do, he started interviewing people to get to the bottom of the problem. See the Ancestors Problem.
One thing that did come out of the exercise is that I began researching the idea of Most Recent Common Ancestor (MRCA). It led to a number of approaches from statistical to molecular evolution markers. I was hoping to write more about it when I had the time. An example of the statistical approach is the article by Joseph Lachance, “Inbreeding, Pedigree Size, and the Most Recent Common Ancestor of Humanity,” J Theor Biol. 2009 November 21; 261(2): 238–247. Online 2009 August 11. doi: 10.1016/j.jtbi.2009.08.006
(Update 5/10/2019) Continue reading