This is a fun problem from the 1949 Eureka magazine.
This is a fun problem from the 1949 Eureka magazine.
“The following problems were set at the Archimedeans’ 1949 Problems Drive. Competitors were allowed five minutes for each question. [This is problem #9.]
A pillar is in the form of a truncated right circular cone. The diameter at the top is 1 ft., at the bottom it is 2 ft. The slant height is 15 ft. A streamer is wound exactly five times round the pillar starting at the top and ending at the bottom. What is the shortest length the streamer can have?”
See the Pillar Wrapping Problem for solution.

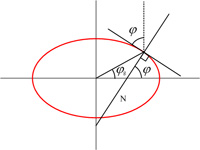
 I thought it might be interesting to explore the mathematics of a common problem with a store-bought HO model train set that contains a collection of straight track segments and fixed-radius curved track segments that form a simple oval. Invariably an initial run of the train has it careening off the track when the train first meets the curved segment after running along the straight track segments.
I thought it might be interesting to explore the mathematics of a common problem with a store-bought HO model train set that contains a collection of straight track segments and fixed-radius curved track segments that form a simple oval. Invariably an initial run of the train has it careening off the track when the train first meets the curved segment after running along the straight track segments.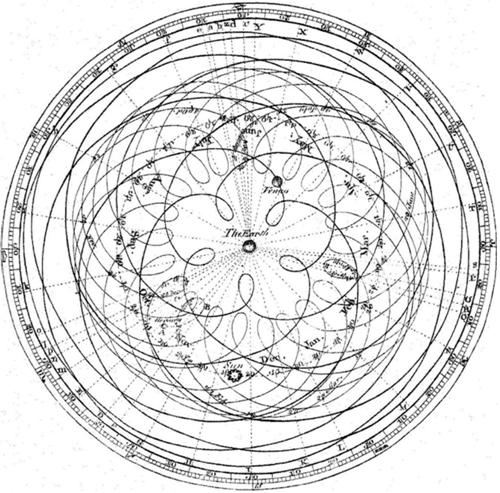 Given the aggravating times, I thought I would vent my frustration by ranting on a somewhat nonsensical topic: “The fact that the earth revolves around the sun, rather than the sun around the earth.” This assertion is often used to separate the supposed dunces from the enlightened. It is put on the same level as “the fact that the earth is round (a sphere) and not flat” with the dunces labeled “flat-earthers.”
Given the aggravating times, I thought I would vent my frustration by ranting on a somewhat nonsensical topic: “The fact that the earth revolves around the sun, rather than the sun around the earth.” This assertion is often used to separate the supposed dunces from the enlightened. It is put on the same level as “the fact that the earth is round (a sphere) and not flat” with the dunces labeled “flat-earthers.”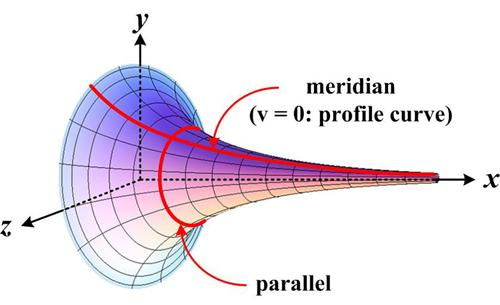 This essay began as an effort to prove Tanya Khovanova’s statement in her article “The Annoyance of Hyperbolic Surfaces” that her crocheted hyperbolic surface had constant (negative) curvature. I discussed Khovanova’s article in my previous essay “
This essay began as an effort to prove Tanya Khovanova’s statement in her article “The Annoyance of Hyperbolic Surfaces” that her crocheted hyperbolic surface had constant (negative) curvature. I discussed Khovanova’s article in my previous essay “ Tanya Khovanova’s recent blog post “The Annoyance of Hyperbolic Surfaces” about crocheting a hyperbolic surface added to the numerous examples of such activity, usually from knitting. Somehow this post caught my attention, in particular about the exponential growth of each added row and the fact that the resulting “surface” had constant negative curvature. I explored the exponential growth in this article and saved the mathematical exploration of the constant negative curvature for a later essay. See
Tanya Khovanova’s recent blog post “The Annoyance of Hyperbolic Surfaces” about crocheting a hyperbolic surface added to the numerous examples of such activity, usually from knitting. Somehow this post caught my attention, in particular about the exponential growth of each added row and the fact that the resulting “surface” had constant negative curvature. I explored the exponential growth in this article and saved the mathematical exploration of the constant negative curvature for a later essay. See 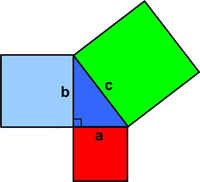 All too frequently I come across the usual statements questioning why non-technical folks should bother studying math. A typical example is the Pythagorean Theorem. People say, “What good is that? I’ll never use it. So why bother?” Ah, the famous “utility” argument – as if everything worthwhile must be “useful.” I thought I would take this “useless” math example par excellence and show that, in fact, it harbors many of the best aspects of mathematics that anyone should find appealing. See the
All too frequently I come across the usual statements questioning why non-technical folks should bother studying math. A typical example is the Pythagorean Theorem. People say, “What good is that? I’ll never use it. So why bother?” Ah, the famous “utility” argument – as if everything worthwhile must be “useful.” I thought I would take this “useless” math example par excellence and show that, in fact, it harbors many of the best aspects of mathematics that anyone should find appealing. See the