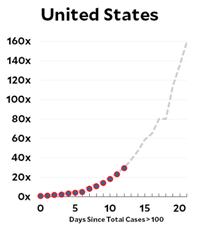
 Given the mathematical nature of this website I feel reluctantly impelled to address the coronavirus pandemic. The mathematics behind the spread of infection is basically the same exponential growth that I discussed in the “Math and Religion” post and has recently been explained by the ever-lucid Grant Sanderson at his 3Blue1Brown website.
Given the mathematical nature of this website I feel reluctantly impelled to address the coronavirus pandemic. The mathematics behind the spread of infection is basically the same exponential growth that I discussed in the “Math and Religion” post and has recently been explained by the ever-lucid Grant Sanderson at his 3Blue1Brown website.
What I wish to draw attention to is the series of posts on the coronavirus by Kevin Drum on his website at Mother Jones. I have collected his recent posts comparing the spread of the virus in various countries and added some mathematical commentary of my own, which is the content of this post.
But the bottom line seems to be that in virtually all the countries, including the US, the virus infection is spreading at the Italian rate of doubling every 4 days! The readers of this website are sufficiently numerate to realize the frightening import of that number. If that weren’t enough, Kevin provides additional posts on the results of the modeling at the Imperial College that are truly nerve-wracking for someone such as myself in the most vulnerable cohort. The only blessing so far seems to be that, for once, the children are spared.
At this time, I don’t have the stomach to keep updating the post as new numbers come in. That may change. I could address the catastrophe of having ignorance and incompetence at the helm of the national ship of state, but it is too depressing.
See the Coronavirus Mathematics
(Updates 3/17/2020, 3/21/2020, 4/17/2020, 9/20/2020, 10/1/2020) Continue reading

 It is a bit presumptuous to think I could reduce the universe of mathematics to some succinct essence, but ever since I first saw a column in Martin Gardner’s Scientific American Mathematical Games in 1967, I thought his example illustrated the essential feature of mathematics, or at least one of its principal attributes. And he posed it in a way that would be accessible to anyone. I especially wanted to credit Martin Gardner, since the idea resurfaced recently, uncredited, in some attractive videos by Katie Steckles and James Grime. (This reminds me of the Borges idea that “eighty years of oblivion are perhaps equal to novelty”.) See the
It is a bit presumptuous to think I could reduce the universe of mathematics to some succinct essence, but ever since I first saw a column in Martin Gardner’s Scientific American Mathematical Games in 1967, I thought his example illustrated the essential feature of mathematics, or at least one of its principal attributes. And he posed it in a way that would be accessible to anyone. I especially wanted to credit Martin Gardner, since the idea resurfaced recently, uncredited, in some attractive videos by Katie Steckles and James Grime. (This reminds me of the Borges idea that “eighty years of oblivion are perhaps equal to novelty”.) See the 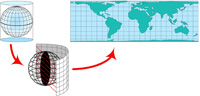 One thing I have always been curious about, but never got around to investigating, is how hard is it to see that the Lambert Equal-Area Projection of a sphere onto a cylinder in fact preserves areas? This 2012 essay attempts to provide an answer. The essay was recently updated to provide a link to the fabulous Youtube site by Grant Sanderson at
One thing I have always been curious about, but never got around to investigating, is how hard is it to see that the Lambert Equal-Area Projection of a sphere onto a cylinder in fact preserves areas? This 2012 essay attempts to provide an answer. The essay was recently updated to provide a link to the fabulous Youtube site by Grant Sanderson at