 One of the books that has stuck with me over the years is Carl Becker’s The Declaration of Independence (1922, reprint 1942), not only for its incredibly clear and beautiful writing but also for its emphasis on the impact of the revolution most prominently caused by Isaac Newton, which was later subsumed under the term Scientific Revolution covering the entire 17th century. A consequence of this remarkable period was the so-called Enlightenment that followed in the 18th century and became the soil from which our nation’s founding ideas and documents sprang. Both these centuries have been further optimistically called the Age of Reason.
One of the books that has stuck with me over the years is Carl Becker’s The Declaration of Independence (1922, reprint 1942), not only for its incredibly clear and beautiful writing but also for its emphasis on the impact of the revolution most prominently caused by Isaac Newton, which was later subsumed under the term Scientific Revolution covering the entire 17th century. A consequence of this remarkable period was the so-called Enlightenment that followed in the 18th century and became the soil from which our nation’s founding ideas and documents sprang. Both these centuries have been further optimistically called the Age of Reason.
Our current times, awash in lies, corruption, and such terms as “alternative facts”, have been characterized as an assault on the rationalism and Enlightenment that shaped our founding. Any revisiting of these origins would seem to be a valuable endeavor to see if they still have validity. What makes Becker’s essay particularly relevant to me is the current pervasiveness of the mathematical view of reality that was launched by Newton some 300 years ago. Becker shows how this new way of thinking spread far beyond the bounds of mathematics and engendered a new “natural rights” philosophy that formed the foundation for the Declaration of Independence. Essentially the idea was that if the behavior of the natural world was based on (mathematical) laws, then so must the behavior of man be based on natural laws.
See Newton and Declaration of Independence
(Updates 10/31/2019, 9/18/2020, 3/9/2024) Steven Strogatz Confirmation, an Atlantic article, Natural Law
Continue reading →
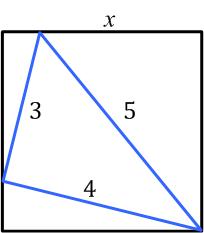 Presh Talwalkar had another interesting problem.
Presh Talwalkar had another interesting problem.
 One of the books that has stuck with me over the years is Carl Becker’s The Declaration of Independence (1922, reprint 1942), not only for its incredibly clear and beautiful writing but also for its emphasis on the impact of the revolution most prominently caused by Isaac Newton, which was later subsumed under the term Scientific Revolution covering the entire 17th century. A consequence of this remarkable period was the so-called Enlightenment that followed in the 18th century and became the soil from which our nation’s founding ideas and documents sprang. Both these centuries have been further optimistically called the Age of Reason.
One of the books that has stuck with me over the years is Carl Becker’s The Declaration of Independence (1922, reprint 1942), not only for its incredibly clear and beautiful writing but also for its emphasis on the impact of the revolution most prominently caused by Isaac Newton, which was later subsumed under the term Scientific Revolution covering the entire 17th century. A consequence of this remarkable period was the so-called Enlightenment that followed in the 18th century and became the soil from which our nation’s founding ideas and documents sprang. Both these centuries have been further optimistically called the Age of Reason. This problem from the 1987 Discover magazine’s Brain Bogglers by Michael Stueben apparently traces back to 1770, though the exact reference is not given.
This problem from the 1987 Discover magazine’s Brain Bogglers by Michael Stueben apparently traces back to 1770, though the exact reference is not given.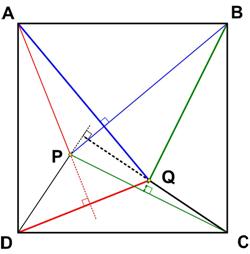 I found this problem from the Math Challenges section of the 2002 Pi in the Sky Canadian math magazine for high school students to be truly astonishing.
I found this problem from the Math Challenges section of the 2002 Pi in the Sky Canadian math magazine for high school students to be truly astonishing. This 2005 four-star problem from Colin Hughes at Maths Challenge is also a bit challenging.
This 2005 four-star problem from Colin Hughes at Maths Challenge is also a bit challenging. This is another stimulating math problem from Colin Hughes’s Maths Challenge website (mathschallenge.net).
This is another stimulating math problem from Colin Hughes’s Maths Challenge website (mathschallenge.net).