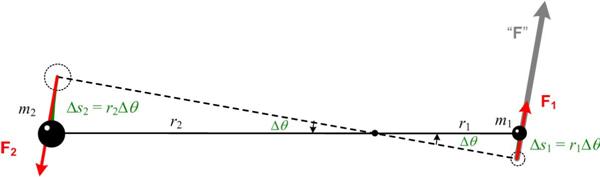
 I have always had a tenuous relationship with the concept of angular momentum, but recently my concerns resurfaced when I did my studies on Kepler, and in particular his “equal areas law” and Newton’s elegant geometric proof. I love the fact that a simple geometric argument, seemingly totally divorced from the physical situation, can provide an explanation for why the line from the Sun to a planet sweeps out equal areas in equal time as the planet orbits the Sun, solely under the influence of the gravitational force between them. However, modern physics books invariably cite the conservation of angular momentum as the “explanation.” I indicated before in my “Kepler’s Laws and Newton’s Laws” essay that this “explanation” irritated me. In this essay I go into detail about my reservations concerning this line of argument. See Angular Momentum.
I have always had a tenuous relationship with the concept of angular momentum, but recently my concerns resurfaced when I did my studies on Kepler, and in particular his “equal areas law” and Newton’s elegant geometric proof. I love the fact that a simple geometric argument, seemingly totally divorced from the physical situation, can provide an explanation for why the line from the Sun to a planet sweeps out equal areas in equal time as the planet orbits the Sun, solely under the influence of the gravitational force between them. However, modern physics books invariably cite the conservation of angular momentum as the “explanation.” I indicated before in my “Kepler’s Laws and Newton’s Laws” essay that this “explanation” irritated me. In this essay I go into detail about my reservations concerning this line of argument. See Angular Momentum.
Tag Archives: Richard Feynman
Meditation on “Is” in Mathematics II – Mathematical Reality
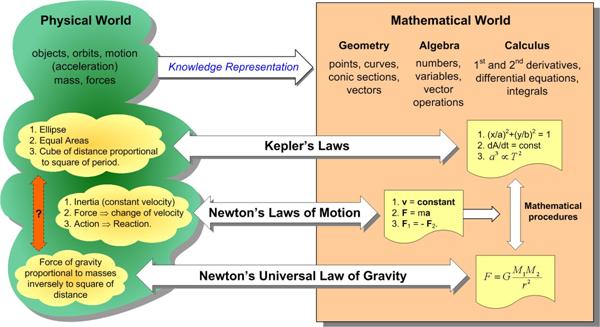 This post continues a meditation on the nature of mathematics begun in Part I. It involves the perennial question about whether mathematics is invented or discovered, and consequently evokes questions about mathematical reality. This subject is probably of little interest to most people, and even most mathematicians. But the extremely heavy involvement of mathematics in the descriptions of quantum mechanics, and the even more mathematically abstruse excursions into ideas such as string theory in an effort to wed quantum mechanics to general relativity, force us to confront the central place mathematics has in “explaining” our physical reality. Of course, this essay has no definitive answers, and leaves the situation as a mystery. See Meditation on “Is” in Mathematics II – Mathematical Reality.
This post continues a meditation on the nature of mathematics begun in Part I. It involves the perennial question about whether mathematics is invented or discovered, and consequently evokes questions about mathematical reality. This subject is probably of little interest to most people, and even most mathematicians. But the extremely heavy involvement of mathematics in the descriptions of quantum mechanics, and the even more mathematically abstruse excursions into ideas such as string theory in an effort to wed quantum mechanics to general relativity, force us to confront the central place mathematics has in “explaining” our physical reality. Of course, this essay has no definitive answers, and leaves the situation as a mystery. See Meditation on “Is” in Mathematics II – Mathematical Reality.
