Tag Archives: Henry Dudeney

The Weight Problem of Bachet de Méziriac

The following is a famous problem of Bachet as recounted by Heinrich Dörrie in his book 100 Great Problems of Elementary Mathematics:

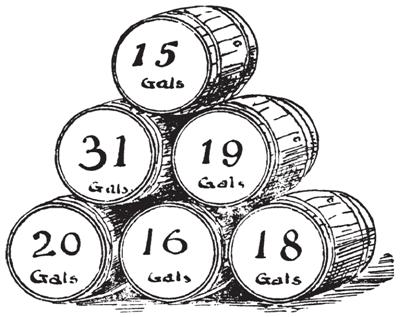
“A merchant had a forty-pound measuring weight that broke into four pieces as the result of a fall. When the pieces were subsequently weighed, it was found that the weight of each piece was a whole number of pounds and that the four pieces could be used [in a balance scale] to weigh every integral weight between 1 and 40 pounds [when we are allowed to put a weight in either of the two pans]. What were the weights of the pieces?

(This problem stems from the French mathematician Claude Gaspard Bachet de Méziriac (1581-1638), who solved it in his famous book Problèmes plaisants et délectables qui se font par les nombres, published in 1624.)”

The problem has a nice solution using ternary numbers.

Answer.

See the Weight Problem of Bachet for a solution.

(Update 4/10/2019) Continue reading →

The Barrel of Beer

This is a great puzzle by H. E. Dudeney involving a very useful technique.

“A man bought an odd lot of wine in barrels and one barrel containing beer. These are shown in the illustration, marked with the number of gallons that each barrel contained. He sold a quantity of the wine to one man and twice the quantity to another, but kept the beer to himself. The puzzle is to point out which barrel contains beer. Can you say which one it is? Of course, the man sold the barrels just as he bought them, without manipulating in any way the contents.”

Answer.

See the Barrel of Beer for an answer.

The Two Errand Boys

This is another puzzle from the Futility Closet that was originally from Henry Dudeney’s Canterbury Puzzles.

“A country baker sent off his boy with a message to the butcher in the next village, and at the same time the butcher sent his boy to the baker. One ran faster than the other, and they were seen to pass at a spot 720 yards from the baker’s shop. Each stopped ten minutes at his destination and then started on the return journey, when it was found that they passed each other at a spot 400 yards from the butcher’s. How far apart are the two tradesmen’s shops? Of course each boy went at a uniform pace throughout.”

Answer.

See the Two Errand Boys for solutions.

Three Jugs Problem

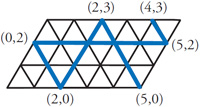Years ago (1967) I read about an interesting solution to the three jugs problem in a book by Nathan Court which involved the idea of a billiard ball traversing a skew billiard table with distributions of the water between the jugs listed along the edges of the table. The ball bounced between solutions until it ended on the desired value. I thought it was very clever, but I really did not understand why it worked. Later I figured out an explanation, which I present here. See the Three Jugs Problem.

  1. Pages:
  3. 1
  4. 2