It is a bit presumptuous to think I could reduce the universe of mathematics to some succinct essence, but ever since I first saw a column in Martin Gardner’s Scientific American Mathematical Games in 1967, I thought his example illustrated the essential feature of mathematics, or at least one of its principal attributes. And he posed it in a way that would be accessible to anyone. I especially wanted to credit Martin Gardner, since the idea resurfaced recently, uncredited, in some attractive videos by Katie Steckles and James Grime. (This reminds me of the Borges idea that “eighty years of oblivion are perhaps equal to novelty”.) See the Essence of Mathematics.
Tag Archives: Eugene Wigner
Meditation on “Is” in Mathematics II – Mathematical Reality
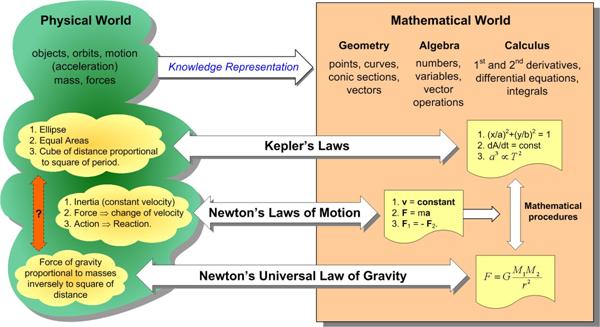This post continues a meditation on the nature of mathematics begun in Part I. It involves the perennial question about whether mathematics is invented or discovered, and consequently evokes questions about mathematical reality. This subject is probably of little interest to most people, and even most mathematicians. But the extremely heavy involvement of mathematics in the descriptions of quantum mechanics, and the even more mathematically abstruse excursions into ideas such as string theory in an effort to wed quantum mechanics to general relativity, force us to confront the central place mathematics has in “explaining” our physical reality. Of course, this essay has no definitive answers, and leaves the situation as a mystery. See Meditation on “Is” in Mathematics II – Mathematical Reality.