It is a bit presumptuous to think I could reduce the universe of mathematics to some succinct essence, but ever since I first saw a column in Martin Gardner’s Scientific American Mathematical Games in 1967, I thought his example illustrated the essential feature of mathematics, or at least one of its principal attributes. And he posed it in a way that would be accessible to anyone. I especially wanted to credit Martin Gardner, since the idea resurfaced recently, uncredited, in some attractive videos by Katie Steckles and James Grime. (This reminds me of the Borges idea that “eighty years of oblivion are perhaps equal to novelty”.) See the Essence of Mathematics.
Tag Archives: Einstein
Lorentz Transformation
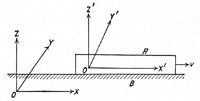Over the years one of the subjects I return to periodically to study is Einstein’s Theory of Relativity, both the Special and General theories. Interest in the Special Theory focused on the derivation of the Lorentz transformations (or contractions). Why did objects appear with different lengths and clocks run at different speeds for observers moving relative to one another? Early on (late 60s) I came across a great explanation in the 1923 book by C. P. Steinmetz. He derived it from two general assumptions of special relativity: (1) that all motion is relative, the motion of the railway train relative to the track being the same as the motion of the track relative to the train, and (2) that the laws of nature, and thus the velocity of light, are the same everywhere. I did not follow his derivation completely, so I produced my own, which I will give here. See the Lorentz Transformation.