This is a puzzle from Talwalkar’s set of “Impossible Puzzles with Surprising Solutions.”

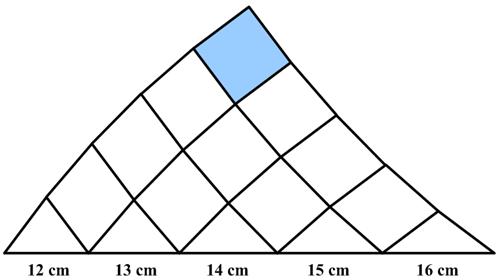
“Call this puzzle the leaning tower of rhombi.

There are 5 isosceles triangles, aligned along their bases, with base lengths of 12, 13, 14, 15, 16 cm. The 10 quadrilaterals above are in rows of 4, 3, 2, and 1. Each quadrilateral is a rhombus, and the top of the tower is a square. What is the area of the square?”

Answer.

See Stacked Rhombuses Puzzle for solutions.