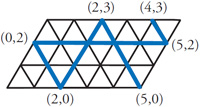
 Years ago (1967) I read about an interesting solution to the three jugs problem in a book by Nathan Court which involved the idea of a billiard ball traversing a skew billiard table with distributions of the water between the jugs listed along the edges of the table. The ball bounced between solutions until it ended on the desired value. I thought it was very clever, but I really did not understand why it worked. Later I figured out an explanation, which I present here. See the Three Jugs Problem.
Years ago (1967) I read about an interesting solution to the three jugs problem in a book by Nathan Court which involved the idea of a billiard ball traversing a skew billiard table with distributions of the water between the jugs listed along the edges of the table. The ball bounced between solutions until it ended on the desired value. I thought it was very clever, but I really did not understand why it worked. Later I figured out an explanation, which I present here. See the Three Jugs Problem.
Meditations on Mathematics
A compendium of puzzles, problems, math inquiries, and math commentary.
