 A while ago James Tanton provided a series of puzzles:
A while ago James Tanton provided a series of puzzles:
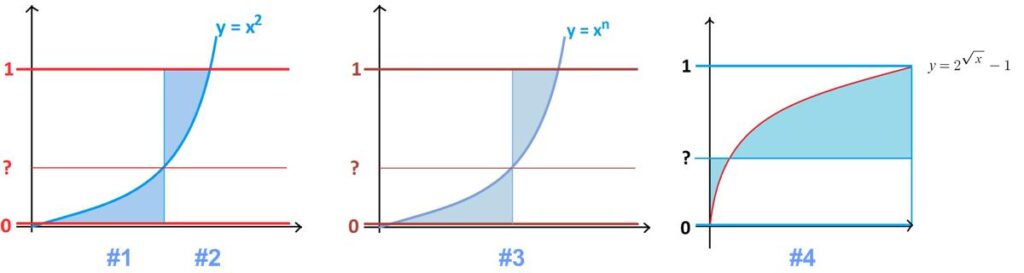
Puzzle #1 At what value between 0 and 1 does a horizontal line at that height produce two regions of equal area as shown on the graph of y = x2?
Puzzle #2 A horizontal line is drawn between the lines y = 0 and y = 1, dividing the graph of y = x2 into two regions as shown. At what height should that line be drawn so that the sum of the areas of these two regions is minimal?
Puzzle #3 A horizontal line is drawn between the lines y = 0 and y = 1, dividing the graph of y = xn into two regions as shown (n > 0). At what height should that line be drawn so that the sum of the areas of these two regions is minimal? Does that height depend on the value of n?
Puzzle #4 What horizontal line drawn between y = 0 and y = 1 on the graph of y = 2√x – 1 minimizes the sum of the two shaded areas shown?
See Double Areas Puzzles for solutions.
