This is an interesting problem from the collection Five Hundred Mathematical Challenges.

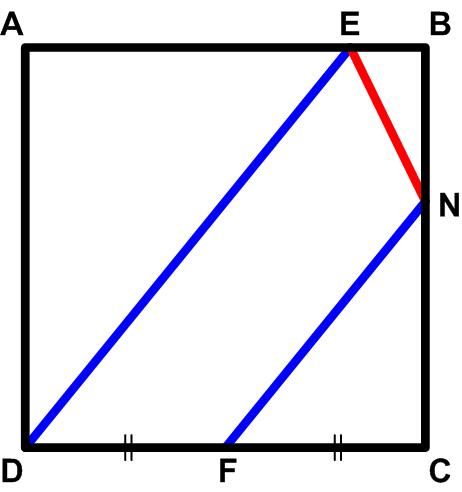
“Problem 251.  Let ABCD be a square, F be the midpoint of DC, and E be any point on AB such that AE > EB.  Determine N on BC such that DE || FN.  Prove that EN is tangent to the inscribed circle of the square.”

See the Parallel Lines Problem.