This is an interesting problem from the 1977 Canadian Math Society’s magazine, Crux Mathematicorum.

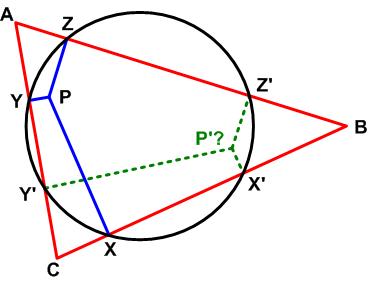
“206. [1977: 10] Proposed by Dan Pedoe, University of Minnesota.

A circle intersects the sides BC, CA and AB of a triangle ABC in the pairs of points X, X’, Y, Y’ and Z, Z’ respectively. If the perpendiculars at X, Y and Z to the respective sides BC, CA and AB are concurrent at a point P, prove that the respective perpendiculars at X’, Y’ and Z’ to the sides BC, CA and AB are concurrent at a point P’.”

See the Twin Intersection Puzzle

Puzzles and Problems: plane geometry, Dan Pedoe, Crux Mathematicorum