 This is another problem from the indefatigable Presh Talwalkar.
This is another problem from the indefatigable Presh Talwalkar.
_ _____Hard Geometry Problem
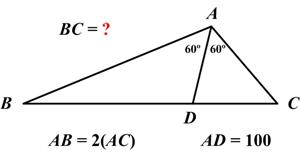
“In triangle ABC above, angle A is bisected into two 60° angles. If AD = 100, and AB = 2(AC), what is the length of BC?”
See Hard Geometric Problem for solutions.
(Update 7/18/2020, 7/20/2020) Alternative Solution
(Update 7/18/2020) I received a solution to the Hard Geometric Problem from
Evander Tandiarrang
Harapan Beliem Wamena (Primary School, Grade 6)
Google maps showed the city of Wamena to be located in Papua New Guinea, Indonesia.
Unfortunately I could not find the exact location of SD Harapan Beliem Elementary school. I did find an undated photo of apparently students, teachers, and parents at the school.

Even though I do not understand the Indonesian language, or any of the 300 different languages spoken by the 200 million population of the country (according to Wikipedia), the universal language of mathematics triumphed, and I was able to verify that Evander Tandiarrang had indeed solved the problem, and in a way that did not involve complex variables, the law of cosines, or the law of sines. The path through the proof displayed an exceptional mastery of the complexities of basic plane geometry. Indonesian prowess in mathematics is legendary, but to find such capability in a 6th grade elementary school student is breathtaking, and a bit intimidating. Nice job.
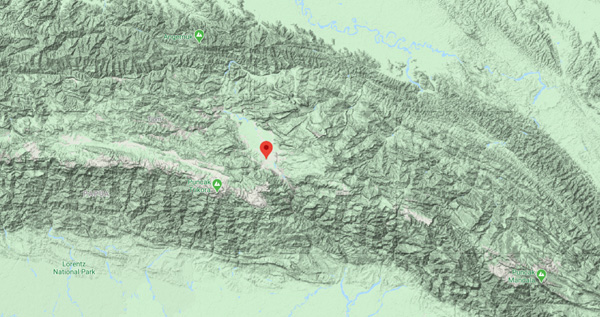
(Update 7/20/2020) I received a response from Evander, who provided me with a photo and location for his school in Wamena (I believe it is the red marker—I think the blue marker is for Wamena). He also writes about himself in very good English. See Evander Tandiarrang Profile.
With all the horror stories about the dangers of the internet, it is extremely gratifying to see an example of how the internet can bring the world together under the rational, universal umbrella of mathematics. It is one of the reasons I am glad to be a mathematician.
These are some photos Evander sent that I missed at first:




Since AD is the angle bisector of angle A,
Let AB=2X and BD=2M
BD/DC=AB/AC=2. So BC=3M.
Apply Cos Law to triangles ABC and ADC,
We get two equations in X and M.
9M^2=7X^2 ….(1) and
M^2= 10000+X^2-100X ….(2)
So;ve (2) quadratic in X and substitute this X in (1).
BC=3M=(Squareroot 7)/2 *300.
Sorry, I did not see the solution by Talwalkar when I gave my solution.
My solution may be canceled.
I originally tried to corroborate your solution and got stuck at the statement BD/DC = 2. It was not obvious to me. But assuming it was true, I was able to confirm the rest of your statements. Then I decided to look at Talwalkar’s solution (it has been over a year since I thought about this), and see that he justifies BD/DC = 2 via the “angle bisector theorem”, which I don’t recall. He then goes to prove it anyway. The proof being non-trivial, I decided I was correct to think the result was not “obvious”. Once I refamiliarized myself with Talwalkar’s solution, I do agree yours was essentially the same (with a few missing steps!). Still, nice job.