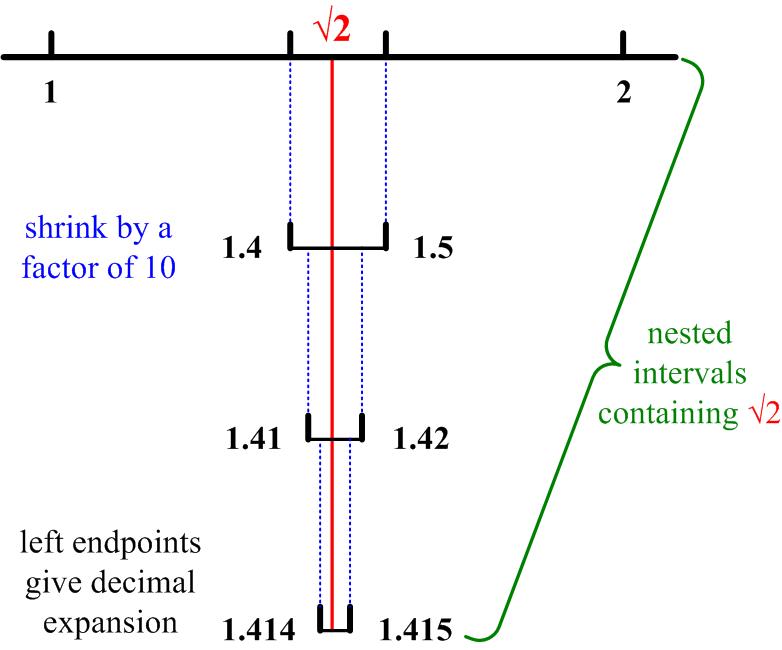
 Probably the most satisfying article I have put together is a recent one on point set topology. An old friend of mine, who studied math and physics in college but ended up getting a doctorate in English, asked me, what was topology? Knowing that there were two main branches of topology (general or point set topology and algebraic topology), I chose to describe point set topology first, especially since it was what I was most familiar with and had worked with most in my graduate work.
Probably the most satisfying article I have put together is a recent one on point set topology. An old friend of mine, who studied math and physics in college but ended up getting a doctorate in English, asked me, what was topology? Knowing that there were two main branches of topology (general or point set topology and algebraic topology), I chose to describe point set topology first, especially since it was what I was most familiar with and had worked with most in my graduate work.
The essay turned out to have a surprising structure more like a musical theme and variations. The theme was the geometric series. I found it to be a wonderful medium to show the evolution of ideas (acting as variations) from the early Greeks (Zeno’s Paradoxes) through the development of calculus, decimal expansions of real numbers, to power series, metric spaces, and finally general topologies.
There was an additional benefit to this series of transformations of an initial idea: one of the major aspects of true mathematics became evident, namely, the extension of an idea into new territories that reveal unexpected connections to other forms of mathematics. Treating complicated functions as points in a topological space was a wonderful idea developed over the end of the 19th and beginning of the 20th centuries and became the basis of the field of functional analysis. See Point Set Topology (revised).
(Update 6/3/2021) Slightly revised version.
I happened to review this article and noticed I made a mistake in my integration example. I have no idea what I was thinking at the time, so I corrected it. As I reviewed the rest of the article, I noticed a bunch of “typos” that would make the text confusing, so I corrected those as well. And finally I rephrased wording in a couple of places to try to make things clearer.
 For a number of years I have collected excerpts that portray mathematical ideas in a literary or philosophical setting. I had occasion to read a few of these on the last day of some math classes I was teaching, since there was no point in introducing a new subject before the final exam.
For a number of years I have collected excerpts that portray mathematical ideas in a literary or philosophical setting. I had occasion to read a few of these on the last day of some math classes I was teaching, since there was no point in introducing a new subject before the final exam.
 The September 2019 Special Issue of Scientific American is a must read. Unfortunately it is behind a paywall, so you should purchase a copy at a store or digitally online. All the articles are fascinating and relevant, and address basic questions of epistemology—how do we know what we know? The first section, “Truth”, is the most pertinent to my thinking, as it covers three subjects I have been pondering for years.
The September 2019 Special Issue of Scientific American is a must read. Unfortunately it is behind a paywall, so you should purchase a copy at a store or digitally online. All the articles are fascinating and relevant, and address basic questions of epistemology—how do we know what we know? The first section, “Truth”, is the most pertinent to my thinking, as it covers three subjects I have been pondering for years.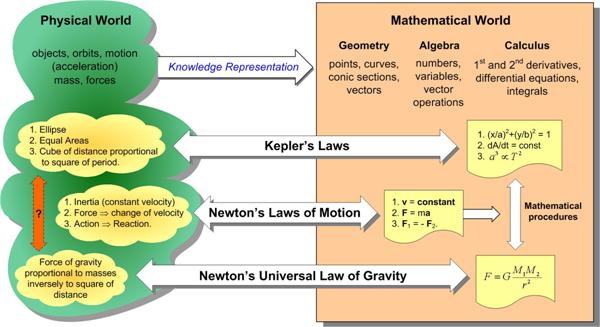 This post continues a meditation on the nature of mathematics begun in Part I. It involves the perennial question about whether mathematics is invented or discovered, and consequently evokes questions about mathematical reality. This subject is probably of little interest to most people, and even most mathematicians. But the extremely heavy involvement of mathematics in the descriptions of quantum mechanics, and the even more mathematically abstruse excursions into ideas such as string theory in an effort to wed quantum mechanics to general relativity, force us to confront the central place mathematics has in “explaining” our physical reality. Of course, this essay has no definitive answers, and leaves the situation as a mystery. See
This post continues a meditation on the nature of mathematics begun in Part I. It involves the perennial question about whether mathematics is invented or discovered, and consequently evokes questions about mathematical reality. This subject is probably of little interest to most people, and even most mathematicians. But the extremely heavy involvement of mathematics in the descriptions of quantum mechanics, and the even more mathematically abstruse excursions into ideas such as string theory in an effort to wed quantum mechanics to general relativity, force us to confront the central place mathematics has in “explaining” our physical reality. Of course, this essay has no definitive answers, and leaves the situation as a mystery. See  This post is the first on a meditation on the nature of mathematics as I see it. I have been thinking about this for some time, and my thoughts were again stimulated by a March 2014 article I read in Slate by Brian Palmer that attempted a popularized explanation of the mathematical concepts associated with Zeno’s Paradox. It was a laudable effort that I applaud. So it is a bit churlish of me to critique it, but I felt its misconceptions got at the heart of some fundamental ideas about mathematics that I wanted to clarify.
This post is the first on a meditation on the nature of mathematics as I see it. I have been thinking about this for some time, and my thoughts were again stimulated by a March 2014 article I read in Slate by Brian Palmer that attempted a popularized explanation of the mathematical concepts associated with Zeno’s Paradox. It was a laudable effort that I applaud. So it is a bit churlish of me to critique it, but I felt its misconceptions got at the heart of some fundamental ideas about mathematics that I wanted to clarify. Probably the most satisfying article I have put together is a recent one on point set topology. An old friend of mine, who studied math and physics in college but ended up getting a doctorate in English, asked me, what was topology? Knowing that there were two main branches of topology (general or point set topology and algebraic topology), I chose to describe point set topology first, especially since it was what I was most familiar with and had worked with most in my graduate work.
Probably the most satisfying article I have put together is a recent one on point set topology. An old friend of mine, who studied math and physics in college but ended up getting a doctorate in English, asked me, what was topology? Knowing that there were two main branches of topology (general or point set topology and algebraic topology), I chose to describe point set topology first, especially since it was what I was most familiar with and had worked with most in my graduate work.