The following is a famous problem of Bachet as recounted by Heinrich Dörrie in his book 100 Great Problems of Elementary Mathematics:
“A merchant had a forty-pound measuring weight that broke into four pieces as the result of a fall. When the pieces were subsequently weighed, it was found that the weight of each piece was a whole number of pounds and that the four pieces could be used [in a balance scale] to weigh every integral weight between 1 and 40 pounds [when we are allowed to put a weight in either of the two pans]. What were the weights of the pieces?
(This problem stems from the French mathematician Claude Gaspard Bachet de Méziriac (1581-1638), who solved it in his famous book Problèmes plaisants et délectables qui se font par les nombres, published in 1624.)”
The problem has a nice solution using ternary numbers.
See the Weight Problem of Bachet for a solution.
(Update 4/10/2019) Continue reading
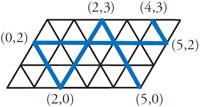Years ago (1967) I read about an interesting solution to the three jugs problem in a book by Nathan Court which involved the idea of a billiard ball traversing a skew billiard table with distributions of the water between the jugs listed along the edges of the table. The ball bounced between solutions until it ended on the desired value. I thought it was very clever, but I really did not understand why it worked. Later I figured out an explanation, which I present here. See the 