Tag Archives: Matthew Scroggs

Cube Roots Problem

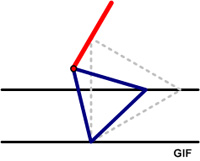
In a June Chalkdust book review of Daniel Griller’s second book, Problem solving in GCSE mathematics, Matthew Scroggs presented the following problem #65 from the book (without a solution):
“Solve _______________”

Scroggs’s initial reaction to the problem was “it took me a while to realise that I even knew how to solve it.”

Mind you, according to Wikipedia, “GCSEs [General Certificate of Secondary Education] were introduced in 1988 [in the UK] to establish a national qualification for those who decided to leave school at 16, without pursuing further academic study towards qualifications such as A-Levels or university degrees.” My personal feeling is that any student who could solve this problem should be encouraged to continue their education with a possible major in a STEM field.

Answer.

See Cube Roots Problem for a solution.

Straight and Narrow Problem

The following interesting behavior was found at the Futility Closet website:

“A pleasing fact from David Wells’ Archimedes Mathematics Education Newsletter: Draw two parallel lines. Fix a point A on one line and move a second point B along the other line. If an equilateral triangle is constructed with these two points as two of its vertices, then as the second point moves, the third vertex C of the triangle will trace out a straight line. Thanks to reader Matthew Scroggs for the tip and the GIF.”

This is rather amazing and cries out for a proof. It also raises the question of how anyone noticed this behavior in the first place. I proved the result with calculus, but I wonder if there is a slicker way that makes it more obvious. See the Straight and Narrow Problem.

(Update 3/25/2019) Continue reading →

Chalkdust Triangle Problem

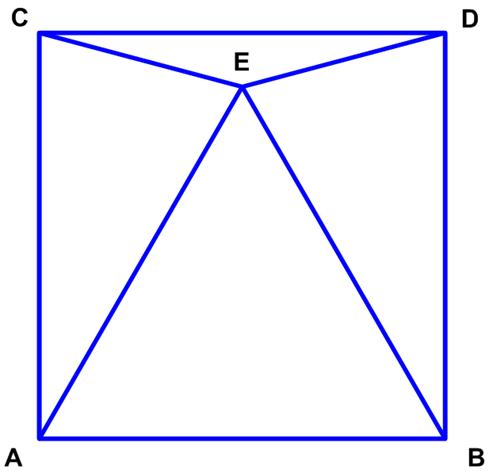The issue 7 of the Chalkdust mathematics magazine had an interesting geometric problem presented by Matthew Scroggs.

“In the diagram, ABDC is a square. Angles ACE and BDE are both 75°. Is triangle ABE equilateral? Why/why not?”

I had a solution, but alas, the Scroggs’s solution was far more elegant.

Answer.

See the Chalkdust Triangle Problem for solutions.

Chalkdust Grid Problem

Normally I don’t care for combinatorial problems, but this problem from Chalkdust Magazine by Matthew Scroggs seemed to bug me enough to try to solve it. It took me a while to see the proper pattern, and then it was rather satisfying.

“You start at A and are allowed to move either to the right or upwards. How many different routes are there to get from A to B?”

Answer.

See the Chalkdust Grid Problem for a solution.