This is a puzzle from Talwalkar’s set of “Impossible Puzzles with Surprising Solutions.”
“Call this puzzle the leaning tower of rhombi.
There are 5 isosceles triangles, aligned along their bases, with base lengths of 12, 13, 14, 15, 16 cm. The 10 quadrilaterals above are in rows of 4, 3, 2, and 1. Each quadrilateral is a rhombus, and the top of the tower is a square. What is the area of the square?”
See Stacked Rhombuses Puzzle for solutions.
Here is a problem from the famous (infamous?) Putnam exam, presented by Presh Talwalkar. Needless to say, I did not solve it in 30 minutes—but at least I solved it (after making a blizzard of arithmetic and trigonometric errors).
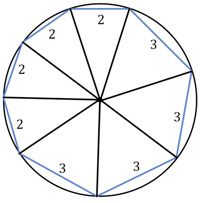
“Today’s problem is from the 1978 test, problem B1 (the easiest of the second set of problems). A convex octagon inscribed in a circle has four consecutive sides of length 3 and four consecutive sides of length 2. Find the area of the octagon.”
My solution is horribly pedestrian and fraught with numerous chances for arithmetic mistakes to derail it, which happened in spades. As I suspected, there was an elegant, “easy” solution (as demonstrated by Talwalkar)—once you thought of it! Again, this is like a Coffin Problem.
See the Putnam Octagon Problem for solutions.
This problem from Futility Closet proved quite challenging.
“University of Illinois mathematician John Wetzel called this one of his favorite problems in geometry. Call a plane arc special if it has length 1 and lies on one side of the line through its end points. Prove that any special arc can be contained in an isosceles right triangle of hypotenuse 1.”
My attempts were futile (maybe that is where the title of the website comes from). Maybe this qualifies for another Coffin Problem. But I did have one little comment about the Futility Closet solution. See Containing an Arc.
These are three “Coffin” Problems posed by Nakul Dawra on his Youtube site GoldPlatedGoof. (Nakul is extraordinarily entertaining and mesmerizing.) The origin of the name is explained, but basically they are problems that have easy or even trivial solutions—once you see the solution. But just contemplating the problem, they seem impossible. The idea was to kill the chances of the pupil taking an (oral) exam with these problems. I was able to solve the first two problems (after a while), but I could not figure out the third. See the Three Coffin Problems.
