Monthly Archives: January 2019

Triangular Boundary Problem

This problem comes from the defunct Wall Street Journal Varsity Math Week collection.

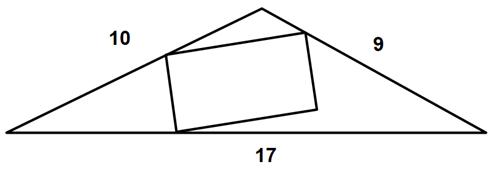
“The coach then shows the team the diagram to the left and asks: What is the maximum area of a rectangle contained entirely within a triangle with sides of 9, 10 and 17?”

I changed the numbers a bit to make my calculations easier, but left the problem otherwise unchanged. When I checked the Varsity Math Week solution, I saw they used a simplifying formula that I could not remember. I also believed their solution left out a justification for the maximal area. Besides an intuitive solution for this, I also included a calculus version.

Answer.

See the Triangular Boundary Problem for solutions.

The Four Travelers Problem

This is another Futility Closet puzzle.

“Four straight roads cross a plain. No two are parallel, and no three meet in a point. On each road is a traveler who moves at some constant speed. If Blue and Red meet each other at their crossroad, and each of them meets Yellow and Green at their respective crossroads, will Yellow and Green necessarily meet at their own crossroad?”

Answer.

I was not able to understand the solution given at first, so I tried to solve the problem on my own. Once I did, I was able to see what the Futility Closet solution was getting at. Certainly diagrams were needed to make sense of it all, and that is what I provided. See the Four Travelers Problem.

  1. Pages:
  3. 1
  4. 2
  5. 3
  6. 4