Tag Archives: David Wells

Regiomontanus 1471 Problem

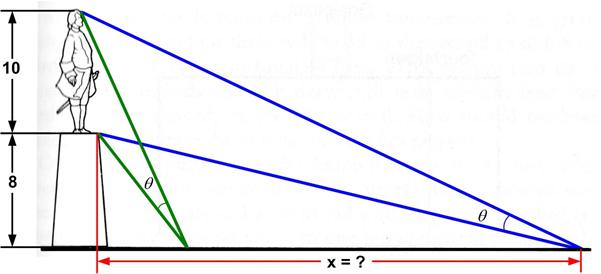
This is an old problem I had seen before. Here is David Wells’s rendition:

“Johannes Müller, named Regiomontanus after the Latin translation of Körnigsberg, his city of birth, later made famous by Euler, proposed this problem in 1471. … it is usually put in this form …: From what distance will a statue on a plinth appear largest to the eye [of a mouse!]? If we approach too close, the statue appears foreshortened, but from a distance it is simply small.”

I have added height numbers in feet for concreteness (as well as the mouse qualification, since the angles are measured from ground level). So the problem is to find the distance x such that the angle is maximal.

Answer.

See the Regiomontanus 1471 Problem for solutions.

Straight and Narrow Problem

The following interesting behavior was found at the Futility Closet website:

“A pleasing fact from David Wells’ Archimedes Mathematics Education Newsletter: Draw two parallel lines. Fix a point A on one line and move a second point B along the other line. If an equilateral triangle is constructed with these two points as two of its vertices, then as the second point moves, the third vertex C of the triangle will trace out a straight line. Thanks to reader Matthew Scroggs for the tip and the GIF.”

This is rather amazing and cries out for a proof. It also raises the question of how anyone noticed this behavior in the first place. I proved the result with calculus, but I wonder if there is a slicker way that makes it more obvious. See the Straight and Narrow Problem.

(Update 3/25/2019) Continue reading →

Keyhole Problem

This is another problem from the Futility Closet website. It turned out to be pretty simple. The idea is to show the length of BC remains the same no matter where A is chosen on its arc of C1. 

(Update 7/1/2020) There is more to this problem than I realized, thanks to a revisit prompted by a question from Deb Jyoti Mitra.  See the revised Keyhole Problem.