 I thought this puzzle, which was included among a set of seven challenges assembled by Presh Talwalkar, would be fairly straight-forward.
I thought this puzzle, which was included among a set of seven challenges assembled by Presh Talwalkar, would be fairly straight-forward.
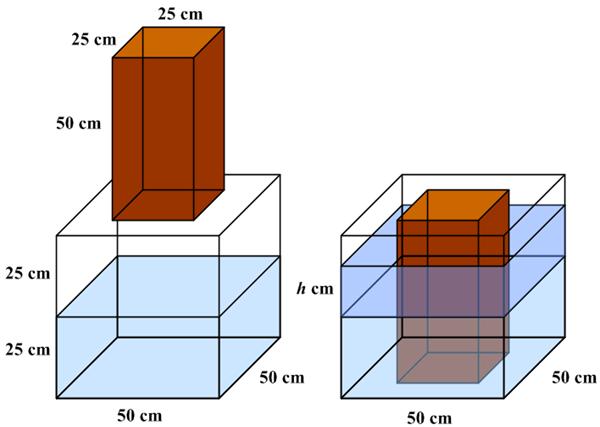
“A cube of 50 cm is filled halfway with water. A rectangular prism with a square base of 25 cm and a height around 50 cm is placed flat onto the base of the cube, as shown. By how much does the water level rise?
Thanks to Fahad Alomaim for the suggestion! This is translated from a Mawhiba curriculum question for 8th grade.”
But I got the wrong answer and found Talwalkar’s solution a bit hard to fathom at first. Looks like I flunked 8th grade.
See Brick in Water Puzzle for solutions.

My approach.
Total water volume =50×50×25= 62500 cc
Let H be final height of water level from the bottom.
The brick volume below the water level
=25×25×H = 625H cc…..(1)
The total volume of submerged brick + water =50×50×H = 2500H cc….(2)
The net volume of water = (2) – (1)
= 2500H – 625H = 1875H
This must equal to original volume of water.
1875H = 62500
H = 33.33 cm
Increase in water level= 33.33-25=8.33 cm.
**********