 The Futility Closet website had the following problem:
The Futility Closet website had the following problem:
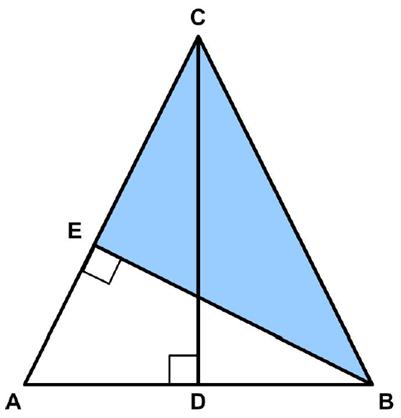
“In isosceles triangle ABC, CD = AB and BE is perpendicular to AC. Show that CEB is a 3-4-5 right triangle.”
See a Triangle Puzzle

 The Futility Closet website had the following problem:
The Futility Closet website had the following problem:
“In isosceles triangle ABC, CD = AB and BE is perpendicular to AC. Show that CEB is a 3-4-5 right triangle.”
See a Triangle Puzzle
Another method.
Let AC=BC=5
From right angled triangle CDB, as BC=5, CD=2*DB we get CD=AB=2*√5
Using cosine rule for the triangle ACB,
cos (C) = (AC^2 + BC^2 – AB^2)/(2*AC*BC)
= [5^2 + 5^2 – (2*√5)^2]/(2*5*5)
= 3/5…..(1)
Also from the right angled triangle CEB,
cos (C)=EC/BC = EC/5….(2)
From (1) and (2),
EC/5 = 3/5 or EC=3….(3)
Hence the remaining side of the right angled triangle CEB must be 4.
Thus the triangle CEB is 3-4-5 triangle.