 For me this turned out to be sort of a challenging problem from the 2025 Math Calendar.
For me this turned out to be sort of a challenging problem from the 2025 Math Calendar.
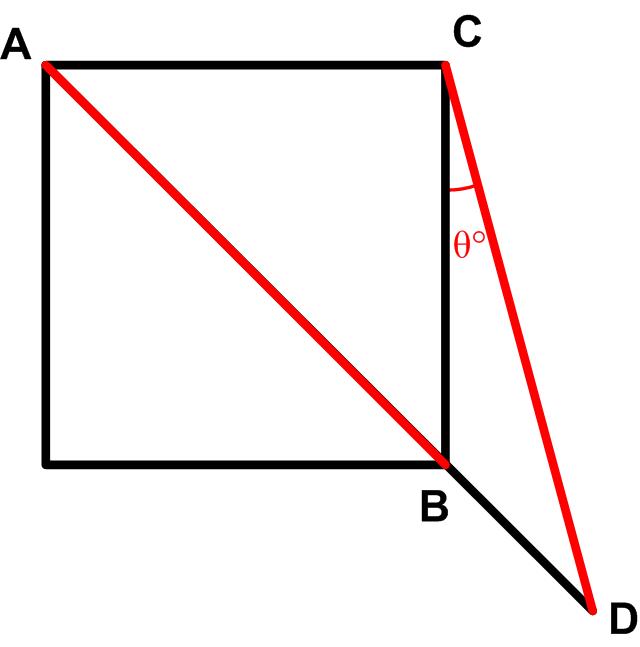
“Given equal line segments AB = CD, what is angle θ in degrees?”
See Elusive Angle for a solution

 For me this turned out to be sort of a challenging problem from the 2025 Math Calendar.
For me this turned out to be sort of a challenging problem from the 2025 Math Calendar.
“Given equal line segments AB = CD, what is angle θ in degrees?”
See Elusive Angle for a solution
Another method.
Let BC = 1. Hence CD=AB= sqrt(2)
Also angle CBD = 180-45=135 deg.
From triangle CBD,
sin(ang BDC) / BC = sin(ang CBD) / CD
sin(ang BDC) / 1 = sin(135) / sqrt(2)
sin(ang BDC) = 1/2
ang BDC= 30 deg
ang BCD = 180 – 135 – 30 = 15 deg.
********
One more method.
Let E be the fourth corner of the square. Join CE and ED. It is easy to show that, the triangle CED is equilateral and hence angle CDE is 60 deg. Also AD is angle bisector of the angle CDE by symmetry.
It implies angle ADC is 30 deg. Since angle CBD is 90+45=135 deg, the third angle BCD, of the triangle CBD, is 15 deg.