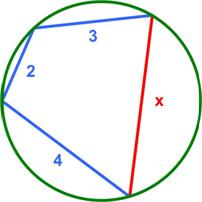
Here is another Brain Bogglers problem from 1987 by Michael Stueben.
“A quadrilateral with sides three, two, and four units in length is inscribed in a circle of diameter five. What’s the length of the fourth side of the quadrilateral?”
Like a number of other Brain Bogglers this problem also uses an insight that makes the solution easy.
See the Quad in Circle Problem for a solution.

area cyclic quadrilateral equals Sqrt((s-a).(s-b).(s-c).(s-d)) so you can alternate the sides without changing the area.
That looks like a result related to Heron’s formula for the area of triangles. I confess to not being familiar with results for cyclic polygons in general, and cyclic quadrilaterals in particular. How would you prove it? (The proof of Heron’s formula is pretty much an arithmetic nightmare in a lot of applications of the Pythagorean Theorem.)