 A recent video by Angela Collier about compound interest reminded me of an effort I did years ago to derive the formulas for interest calculations, especially for installment payments on a loan like a mortgage. In the process I showed where Euler’s constant e can show up. I thought I would resurrect the material, even though I imagine modern texts now provide the information (I couldn’t easily locate it back then).
A recent video by Angela Collier about compound interest reminded me of an effort I did years ago to derive the formulas for interest calculations, especially for installment payments on a loan like a mortgage. In the process I showed where Euler’s constant e can show up. I thought I would resurrect the material, even though I imagine modern texts now provide the information (I couldn’t easily locate it back then).
Category Archives: Math Inquiries
Yet Another Sum
 This is another challenging sum from the 2024 Math Calendar.
This is another challenging sum from the 2024 Math Calendar.
“Find x where x = et and
 ”
”
As before, recall that all the answers are integer days of the month.
See Yet Another Sum for a solution.
Mystery Curve Puzzle
 Here is another problem from BL’s Weekly Math Games.
Here is another problem from BL’s Weekly Math Games.
“For every point P on y = 2x2, areas A and B are equal. Find the equation for curve C.”
See Mystery Curve Puzzle for a solution
Double Areas Puzzles
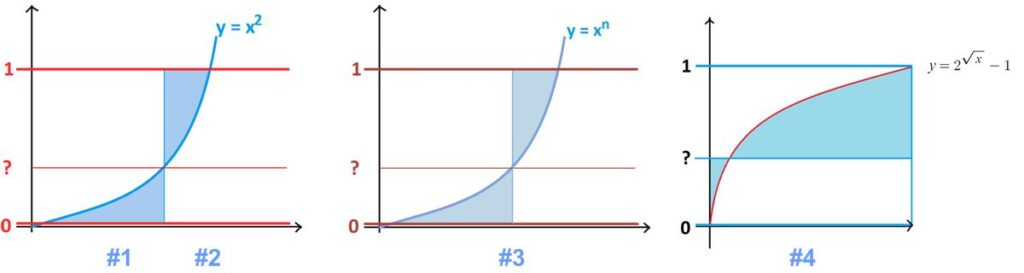 A while ago James Tanton provided a series of puzzles:
A while ago James Tanton provided a series of puzzles:
Puzzle #1 At what value between 0 and 1 does a horizontal line at that height produce two regions of equal area as shown on the graph of y = x2?
Puzzle #2 A horizontal line is drawn between the lines y = 0 and y = 1, dividing the graph of y = x2 into two regions as shown. At what height should that line be drawn so that the sum of the areas of these two regions is minimal?
Puzzle #3 A horizontal line is drawn between the lines y = 0 and y = 1, dividing the graph of y = xn into two regions as shown (n > 0). At what height should that line be drawn so that the sum of the areas of these two regions is minimal? Does that height depend on the value of n?
Puzzle #4 What horizontal line drawn between y = 0 and y = 1 on the graph of y = 2√x – 1 minimizes the sum of the two shaded areas shown?
See Double Areas Puzzles for solutions.
Special Log Sum
 Here is a fairly computationally challenging 1994 AIME problem .
Here is a fairly computationally challenging 1994 AIME problem .
“Find the positive integer n for which
⌊log2 1⌋ + ⌊log2 2⌋ + ⌊log2 3⌋ + … + ⌊log2 n⌋ = 1994.
where for real x, ⌊x⌋ is the greatest integer ≤ x.”
There is some fussy consideration of indices.
See the Special Log Sum for a solution.
Amazing Root Problem
 Well, I discovered that the 2024 Math Calendar has some interesting problems, so I guess things will limp along for a while. This is a challenging but imaginative problem from the calendar.
Well, I discovered that the 2024 Math Calendar has some interesting problems, so I guess things will limp along for a while. This is a challenging but imaginative problem from the calendar.
_______________
As before, recall that all the answers are integer days of the month.
See the Amazing Root Problem for a solution.
Another Challenging Sum
 This is yet another series offered by Presh Talwalkar.
This is yet another series offered by Presh Talwalkar.
“What is the value of the following sum?
____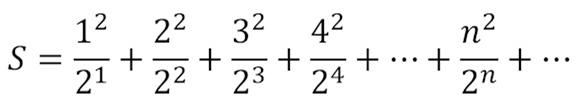
Talwalkar gives hints for three possible approaches to the solution.
See Another Challenging Sum for solutions.
Elliptic Circles
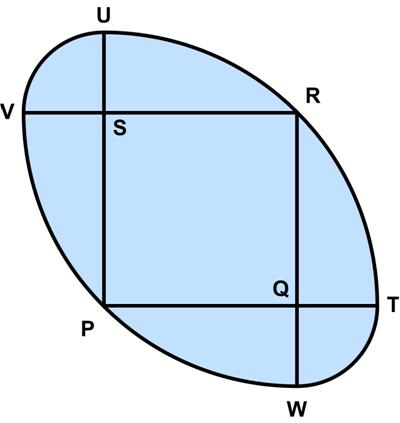 Here is another UKMT Senior Challenge problem for 2017.
Here is another UKMT Senior Challenge problem for 2017.
“The diagram shows a square PQRS with edges of length 1, and four arcs, each of which is a quarter of a circle. Arc TRU has centre P; arc VPW has centre R; arc UV has centre S; and arc WT has centre Q.
What is the length of the perimeter of the shaded region?
A_6___B_(2√2 – 1)π___C_(√2 – 1/2)π ___D_2___E_(3√2 – 2)π”
See Elliptic Circles for a solution.
Amazing Identity
 This is a most surprising and amazing identity from the 1965 Polish Mathematical Olympiads.
This is a most surprising and amazing identity from the 1965 Polish Mathematical Olympiads.
“31. Prove that if n is a natural number, then we have
(√2 – 1)n = √m – √(m – 1),
where m is a natural number.”
Here, natural numbers are 1, 2, 3, …
I found it to be quite challenging, as all the Polish Math Olympiad problems seem to be.
See the Amazing Identity
The Tired Messenger Problem
 Here is another challenging problem from the Polish Mathematical Olympiads. Its generality will cause more thought than for a simpler, specific problem.
Here is another challenging problem from the Polish Mathematical Olympiads. Its generality will cause more thought than for a simpler, specific problem.
“A cyclist sets off from point O and rides with constant velocity v along a rectilinear highway. A messenger, who is at a distance a from point O and at a distance b from the highway, wants to deliver a letter to the cyclist. What is the minimum velocity with which the messenger should run in order to attain his objective?”
See the Tired Messenger Problem
(Update 1/29/2025) Dan Steinitz Solution
Dan Steinitz from Israel has sent an elegant solution that only involves vectors and geometry without calculus. I have edited slightly his email and added excerpts from his whiteboard solution, though without the Hebrew annotations, which unfortunately I cannot read. But that is the glory of the universal language of mathematics: it can be read and understood in any language.
