Tag Archives: plane geometry

Straight and Narrow Problem

The following interesting behavior was found at the Futility Closet website:

“A pleasing fact from David Wells’ Archimedes Mathematics Education Newsletter: Draw two parallel lines. Fix a point A on one line and move a second point B along the other line. If an equilateral triangle is constructed with these two points as two of its vertices, then as the second point moves, the third vertex C of the triangle will trace out a straight line. Thanks to reader Matthew Scroggs for the tip and the GIF.”

This is rather amazing and cries out for a proof. It also raises the question of how anyone noticed this behavior in the first place. I proved the result with calculus, but I wonder if there is a slicker way that makes it more obvious. See the Straight and Narrow Problem.

(Update 3/25/2019) Continue reading →

River Crossing

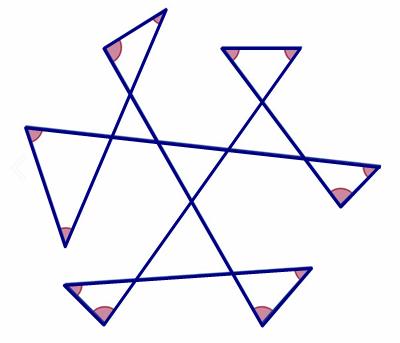
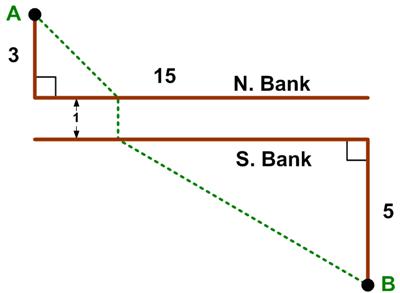This is a riff on a classic problem, given in Challenging Problems in Algebra.

“N. Bank and S. Bank are, respectively, the north and south banks of a river with a uniform width of one mile. Town A is 3 miles north of N. Bank, town B is 5 miles south of S. Bank and 15 miles east of A. If crossing at the river banks is only at right angles to the banks, find the length of the shortest path from A to B.

Challenge. If the rate of land travel is uniformly 8 mph, and the rowing rate on the river is 1 2/3 mph (in still water) with a west to east current of 1 1/3 mph, find the shortest time it takes to go from A to B. [The path across the river must still be perpendicular to the banks.]”

Answer.

See the River Crossing for a solution.

Chalkdust Triangle Problem

The issue 7 of the Chalkdust mathematics magazine had an interesting geometric problem presented by Matthew Scroggs.

“In the diagram, ABDC is a square. Angles ACE and BDE are both 75°. Is triangle ABE equilateral? Why/why not?”

I had a solution, but alas, the Scroggs’s solution was far more elegant.

Answer.

See the Chalkdust Triangle Problem for solutions.

Star Sum of Angles

This problem posted by Presh Talwalkar offers a variety of solutions, but I didn’t quite see my favorite approach for such problems. So I thought I would add it to the mix.

“Thanks to Nikhil Patro from India for suggesting this! What is the sum of the corner angles in a regular 5-sided star? What is a + b + c + d + e = ? Here’s a bonus problem: if the star is not regular, what is a + b + c + d + e = ?”

Answer.

See Star Sum of Angles for solutions.

Containing an Arc

This problem from Futility Closet proved quite challenging.

“University of Illinois mathematician John Wetzel called this one of his favorite problems in geometry. Call a plane arc special if it has length 1 and lies on one side of the line through its end points. Prove that any special arc can be contained in an isosceles right triangle of hypotenuse 1.”

My attempts were futile (maybe that is where the title of the website comes from). Maybe this qualifies for another Coffin Problem. But I did have one little comment about the Futility Closet solution. See Containing an Arc.

Three Coffin Problems

These are three “Coffin” Problems posed by Nakul Dawra on his Youtube site GoldPlatedGoof. (Nakul is extraordinarily entertaining and mesmerizing.) The origin of the name is explained, but basically they are problems that have easy or even trivial solutions—once you see the solution. But just contemplating the problem, they seem impossible. The idea was to kill the chances of the pupil taking an (oral) exam with these problems. I was able to solve the first two problems (after a while), but I could not figure out the third. See the Three Coffin Problems.

  1. Pages:
  3. 1
  4. ...
  5. 8
  6. 9
  7. 10
  8. 11
  9. 12
  10. 13
  11. 14
  12. 15