Tag Archives: plane geometry

Six Squares Problem

This is a problem from the UKMT Senior Challenge for 2001. (It has been slightly edited to reflect the colors I added to the diagram.)

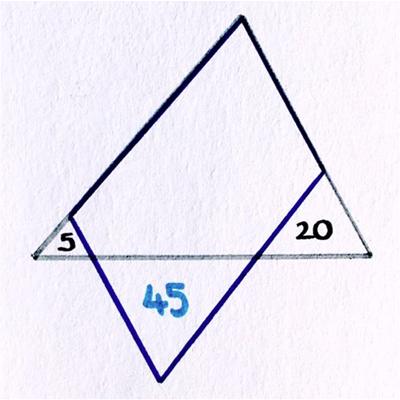
“The [arbitrary] blue triangle is drawn, and a square is drawn on each of its edges. The three green triangles are then formed by drawing their lines which join vertices of the squares and a square is now drawn on each of these three lines. The total area of the original three squares is A1, and the total area of the three new squares is A2. Given that A2 = k A1, then

_____A_ k = 1_____B_ k = 3/2_____C_ k = 2_____D_ k = 3_____E_ more information is needed.”

I solved this problem using a Polya principle to simplify the situation, but UKMT’s solution was direct (and more complicated).

Answer.

See the Six Squares Problem for solutions.

Triangle Acute-Angle Problem

Catriona Shearer retweeted the following problem from Antonio Rinaldi‏ @rinaldi6109

“My little contribution to @Cshearer41 October 7, 2018
A point D is randomly chosen inside the equilateral triangle ABC. Determine the probability that the triangle ABD is acute-angled.”

Answer.

See Triangle Acute-Angle Problem for a solution.

Parallelogram Cosine Problem

Another challenging problem from Presh Talwalkar. I certainly could not have solved it on a timed test at the age of 16.

“One Of The Hardest GCSE Test Questions – How To Solve The Cosine Problem

Construct a hexagon from two congruent parallelograms as shown. Given BP = BQ = 10, solve for the cosine of PBQ in terms of x.

This comes from the 2017 GCSE exam, and it confused many people. I received many requests to solve this problem, and I thank Tom, Ben, and James for suggesting it to me.”

Answer.

See the Parallelogram Cosine Problem for solutions.

Kissing Angles

I really was trying to stop including Catriona Shearer’s problems, since they are probably all well-known and popular by now. But this is another virtually one-step-solution problem that again seems impossible at first. Many of her problems entail more steps, but I am especially intrigued by the one-step problems.

“What’s the sum of the two marked angles?”

Answer.

See Kissing Angles for a solution.

Two Block Incline Puzzle

Since everyone by now who has any interest has gone directly to Catriona Shearer’s Twitter account for geometric puzzles, I was not going to include any more. But this one with its one-step solution is too fine to ignore and belongs with the “5 Problem” as one of the most elegant.

“Two squares sit on the hypotenuse of a right-angled triangle. What’s the angle?”

Answer.

See the Two Block Incline Puzzle for a solution.

(Update 4/26/2019) Continue reading →

Magic Parallelogram

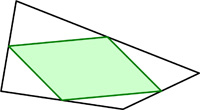I came across this problem in Alfred Posamentier’s book, but I remember I had seen it a couple of places before and had never thought to solve it. At first, it seems like magic.

In any convex quadrilateral (line between any two points in the quadrilateral lies entirely inside the quadrilateral) inscribe a second convex quadrilateral with its vertices on the midpoints of the sides of the first quadrilateral. Show that the inscribed quadrilateral must be a parallelogram.

See the Magic Parallelogram.

(Update 5/15/2020) Continue reading →

Putnam Octagon Problem

Here is a problem from the famous (infamous?) Putnam exam, presented by Presh Talwalkar. Needless to say, I did not solve it in 30 minutes—but at least I solved it (after making a blizzard of arithmetic and trigonometric errors).

“Today’s problem is from the 1978 test, problem B1 (the easiest of the second set of problems). A convex octagon inscribed in a circle has four consecutive sides of length 3 and four consecutive sides of length 2. Find the area of the octagon.”

My solution is horribly pedestrian and fraught with numerous chances for arithmetic mistakes to derail it, which happened in spades. As I suspected, there was an elegant, “easy” solution (as demonstrated by Talwalkar)—once you thought of it! Again, this is like a Coffin Problem.

Answer.

See the Putnam Octagon Problem for solutions.

Conical Bottle Problem

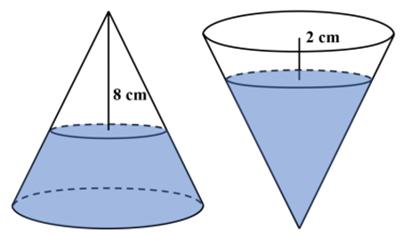I was astonished that this problem was suitable for 8th graders. First of all the formula for the volume of a cone is one of the least-remembered of formulas, and I certainly never remember it. So my only viable approach was calculus, which is probably not a suitable solution for an 8th grader.

Presh Talwalkar: “This was sent to me as a competition problem for 8th graders, so it would be a challenge problem for students aged 12 to 13. When a conical bottle rests on its flat base, the water in the bottle is 8 cm from its vertex. When the same conical bottle is turned upside down, the water level is 2 cm from its base. What is the height of the bottle? (Note “conical” refers to a right circular cone as is common usage.) I at first thought this problem was impossible. But it actually can be solved.”

Answer.

See the Conical Bottle Problem for solutions.

Regiomontanus 1471 Problem

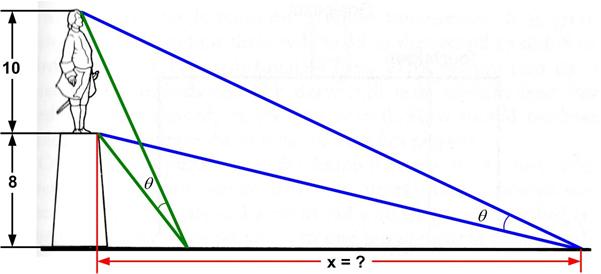This is an old problem I had seen before. Here is David Wells’s rendition:

“Johannes Müller, named Regiomontanus after the Latin translation of Körnigsberg, his city of birth, later made famous by Euler, proposed this problem in 1471. … it is usually put in this form …: From what distance will a statue on a plinth appear largest to the eye [of a mouse!]? If we approach too close, the statue appears foreshortened, but from a distance it is simply small.”

I have added height numbers in feet for concreteness (as well as the mouse qualification, since the angles are measured from ground level). So the problem is to find the distance x such that the angle is maximal.

Answer.

See the Regiomontanus 1471 Problem for solutions.

Parallelogram Problem

Catriona Shearer has come up with another challenging but elegant geometric problem. In some ways, it is similar to the famous Russian Coffin Problems that have an obvious solution—once you see it—but initially seem impenetrable. I really marvel at Catriona Shearer’s ability to come up with these problems.

“What’s the area of the parallelogram?”

Answer.

See the Parallelogram Problem for a solution.

  1. Pages:
  3. 1
  4. ...
  5. 8
  6. 9
  7. 10
  8. 11
  9. 12
  10. 13
  11. 14
  12. 15