Category Archives: Puzzles and Problems

Two Trains – London to Liverpool

This is another train puzzle from H. E. Dudeney, which is fairly straight-forward.

“I put this little question to a stationmaster, and his correct answer was so prompt that I am convinced there is no necessity to seek talented railway officials in America or elsewhere. Two trains start at the same time, one from London to Liverpool, the other from Liverpool to London. If they arrive at their destinations one hour and four hours respectively after passing one another, how much faster is one train running than the other?”

Answer.

See Two Trains – London to Liverpool for a solution.

Challenging Sum

Here is a problem from the UKMT Senior (17-18 year-old) Mathematics Challenge for 2009:

“Four positive integers a, b, c, and d are such that

abcd + abc + bcd + cda + dab + ab + bc + cd + da + ac + bd + a + b + c + d = 2009.

What is the value of a + b + c + d?

A 73_________B 75_________C 77_________D 79_________E 81”

Answer.

See the Challenging Sum for a solution.

(Update 4/17/2019) Continue reading →

Two Block Incline Puzzle

Since everyone by now who has any interest has gone directly to Catriona Shearer’s Twitter account for geometric puzzles, I was not going to include any more. But this one with its one-step solution is too fine to ignore and belongs with the “5 Problem” as one of the most elegant.

“Two squares sit on the hypotenuse of a right-angled triangle. What’s the angle?”

Answer.

See the Two Block Incline Puzzle for a solution.

(Update 4/26/2019) Continue reading →

Magic Parallelogram

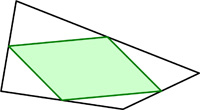I came across this problem in Alfred Posamentier’s book, but I remember I had seen it a couple of places before and had never thought to solve it. At first, it seems like magic.

In any convex quadrilateral (line between any two points in the quadrilateral lies entirely inside the quadrilateral) inscribe a second convex quadrilateral with its vertices on the midpoints of the sides of the first quadrilateral. Show that the inscribed quadrilateral must be a parallelogram.

See the Magic Parallelogram.

(Update 5/15/2020) Continue reading →

Putnam Octagon Problem

Here is a problem from the famous (infamous?) Putnam exam, presented by Presh Talwalkar. Needless to say, I did not solve it in 30 minutes—but at least I solved it (after making a blizzard of arithmetic and trigonometric errors).

“Today’s problem is from the 1978 test, problem B1 (the easiest of the second set of problems). A convex octagon inscribed in a circle has four consecutive sides of length 3 and four consecutive sides of length 2. Find the area of the octagon.”

My solution is horribly pedestrian and fraught with numerous chances for arithmetic mistakes to derail it, which happened in spades. As I suspected, there was an elegant, “easy” solution (as demonstrated by Talwalkar)—once you thought of it! Again, this is like a Coffin Problem.

Answer.

See the Putnam Octagon Problem for solutions.

Two Trains – Passing in the Night

This is one of H. E. Dudeney’s train puzzles.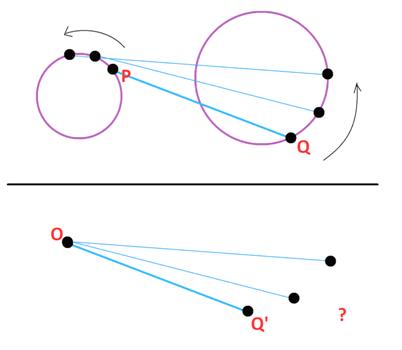

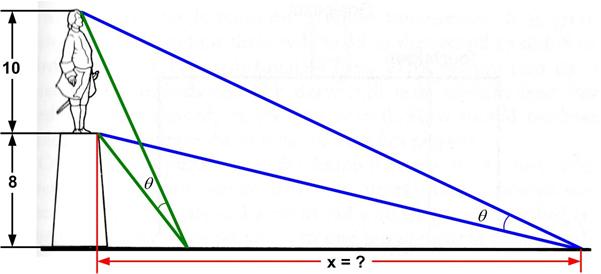“Two railway trains, one four hundred feet long and the other two hundred feet long, ran on parallel rails. It was found that when they went in opposite directions they passed each other in five seconds, but when they ran in the same direction the faster train would pass the other in fifteen seconds. A curious passenger worked out from these facts the rate per hour at which each train ran. Can the reader discover the correct answer? Of course, each train ran with a uniform velocity.”

Answer.

See Two Trains – Passing in the Night for a solution.

Regiomontanus 1471 Problem

This is an old problem I had seen before. Here is David Wells’s rendition:

“Johannes Müller, named Regiomontanus after the Latin translation of Körnigsberg, his city of birth, later made famous by Euler, proposed this problem in 1471. … it is usually put in this form …: From what distance will a statue on a plinth appear largest to the eye [of a mouse!]? If we approach too close, the statue appears foreshortened, but from a distance it is simply small.”

I have added height numbers in feet for concreteness (as well as the mouse qualification, since the angles are measured from ground level). So the problem is to find the distance x such that the angle is maximal.

Answer.

See the Regiomontanus 1471 Problem for solutions.

Parallelogram Problem

Catriona Shearer has come up with another challenging but elegant geometric problem. In some ways, it is similar to the famous Russian Coffin Problems that have an obvious solution—once you see it—but initially seem impenetrable. I really marvel at Catriona Shearer’s ability to come up with these problems.

“What’s the area of the parallelogram?”

Answer.

See the Parallelogram Problem for a solution.

Counterfeit Coin in Base 3

Futility Closet presented a nifty method of solving the “counterfeit coin in 12 coins” problem in a way I had not seen before by mapping the problem into numbers in base 3. It wasn’t immediately clear to me how their solution worked, so I decided to write up my own explanation.

Futility Closet: “You have 12 coins that appear identical. Eleven have the same weight, but one is either heavier or lighter than the others. How can you identify it, and determine whether it’s heavy or light, in just three weighings in a balance scale? This is a classic puzzle, but in 1992 Washington State University mathematician Calvin T. Long found a solution ‘that appears little short of magic.’ ”

See Counterfeit Coin in Base 3.

  1. Pages:
  3. 1
  4. ...
  5. 26
  6. 27
  7. 28
  8. 29
  9. 30
  10. 31
  11. 32
  12. 33