 Here is a seemingly simple problem from Futility Closet.
Here is a seemingly simple problem from Futility Closet.
“A quickie from Peter Winkler’s Mathematical Puzzles, 2021: Can West Virginia be inscribed in a square? That is, is it possible to draw some square each of whose four sides is tangent to this shape?”
Technically we might rephrase this as, can we inscribe a flat map of West Virginia in a square, since the boundary of most states is probably not differentiable everywhere, that is, has a tangent everywhere.
But the real significance of the problem is that it is an example of an “existence proof”, which in mathematics refers to a proof that asserts the existence of a solution to a problem, but does not (or cannot) produce the solution itself. These proofs are second in delight only to the “impossible proofs” which prove that something is impossible, such as trisecting an angle solely with ruler and compass.
Here is another classic example (whose origin I don’t recall). Consider the temperatures of the earth around the equator. At any given instant of time there must be at least two antipodal points that have the same temperature. (Antipodal points are the opposite ends of a diameter through the center of the earth.)
See Existence Proofs (revised)
(Update 10/2/2021) I fixed a minor typo: “tail” should have been “head”

 Here is a challenging problem from the Polish Mathematical Olympiads published in 1960.
Here is a challenging problem from the Polish Mathematical Olympiads published in 1960.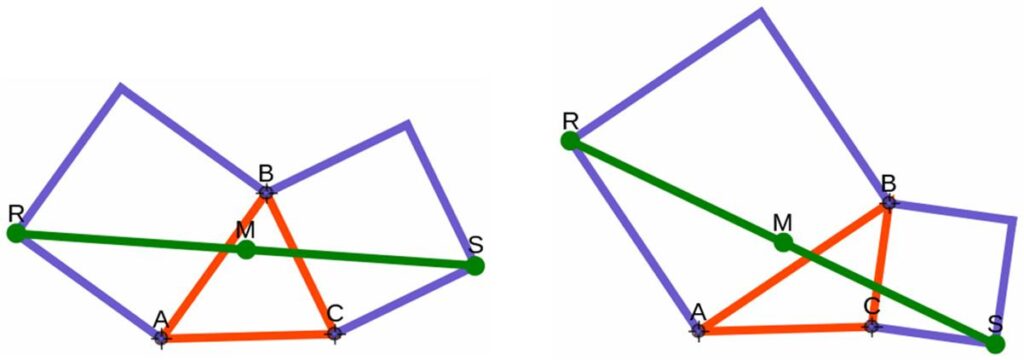
 Here is surprising problem from the 1875 The Analyst
Here is surprising problem from the 1875 The Analyst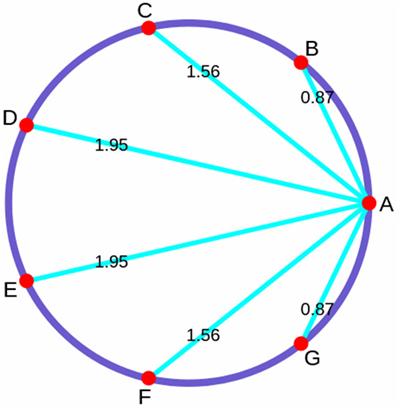 Futility Closet
Futility Closet Here is another challenging problem from the first issue of the 1874 The Analyst, which also appears in Benjamin Wardhaugh’s book.
Here is another challenging problem from the first issue of the 1874 The Analyst, which also appears in Benjamin Wardhaugh’s book. Here is a fairly straight-forward problem from 500 Mathematical Challenges.
Here is a fairly straight-forward problem from 500 Mathematical Challenges. Here is another problem from the 2020 Math Calendar.
Here is another problem from the 2020 Math Calendar.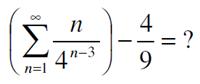
 The following problem comes from a 1961 exam set collected by Ed Barbeau of the University of Toronto. The discontinued exams (by 2003) were for 5th year Ontario high school students seeking entrance and scholarships for the second year at a university.
The following problem comes from a 1961 exam set collected by Ed Barbeau of the University of Toronto. The discontinued exams (by 2003) were for 5th year Ontario high school students seeking entrance and scholarships for the second year at a university. This is another problem from the 2020 Math Calendar.
This is another problem from the 2020 Math Calendar.