This is a nifty problem from Presh Talwakar.
“This is adapted from the 1994 Putnam, A2. Thanks to Nirman for the suggestion!
Let R be the region in the first quadrant bounded by the x-axis, the line y = x/2, and the ellipse x2/9 + y2 = 1. Let R‘ be the region in the first quadrant bounded by the y-axis, the line y = mx and the ellipse. Find the value of m such that R and R‘ have the same area.”
See the Putnam Ellipse Areas Problem for solution.
This is a Catriona Agg problem presented by itself, since it turned out to be the most challenging one I ever tried. Usually I can solve her problems in a few minutes or maybe hours, or sometimes days if they are especially challenging. But this problem has taken me weeks and I had to rely on a non-geometric argument. The problem is full of fascinating and unexpected relationships, but I couldn’t find a way to use them to prove the answer.
See the Curious Sunbeam Problem
(Update 5/5/2023, 7/22/2025) Alternative Solutions Continue reading
Here is yet another (belated) collection of beautiful geometric problems from Catriona Agg (née Shearer).
This is a straight-forward problem from the Scottish Mathematical Council (SMC) Senior Mathematics Challenge.
“A circle has radius 1 cm and AB is a diameter. Two circular arcs of equal radius are drawn with centres A and B. These arcs meet on the circle as shown. Calculate the shaded area.”
There are several possible approaches and the SMC offers two examples.
See the Moon Quarters Problem for solution.
Here is a familiar puzzle from the Mathigon Puzzle Calendars for 2021.
“Given a line and two points A and B, which point P on the line forms the largest angle APB?”
See the Max Angle Puzzle
An excellent application of the solution to this puzzle can be found at Numberphile, where Ben Sparks explains an optimal rugby goal-kicking strategy.
(Update 3/23/2023) Solution Construction
This is a fairly simple problem from Futility Closet, which is currently under a hiatus.
“Robert Bilinski proposed this problem in the April 2006 issue of Crux Mathematicorum. On square ABCD, two equilateral triangles are constructed, ABE internally and BCF externally, as shown. Prove that D, E, and F are collinear.”
See Line Work
This is a nice puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings.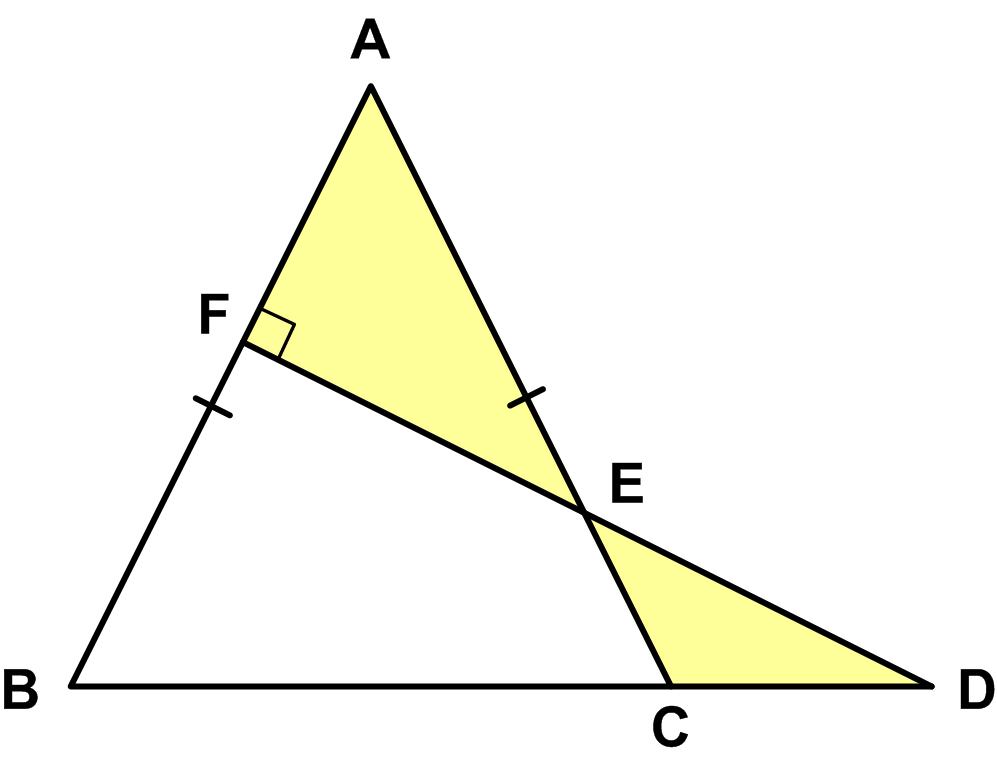
“In the picture does the green rectangle cover more or less than half of the [congruent] red rectangle?”
It is evident from the problem solution that the two rectangles are the same, so I made it explicit.
See the Covering Rectangle Puzzle for solutions.
I found this problem from the 1981 Canadian Math Society’s magazine, Crux Mathematicorum, to be quite challenging.
“Proposed by Kaidy Tan, Fukien Teachers’ University, Foochow, Fukien, China.
An isosceles triangle has vertex A and base BC. Through a point F on AB, a perpendicular to AB is drawn to meet AC in E and BC produced in D. Prove synthetically that
Area of AFE = 2 Area of CDE if and only if AF = CD.”
See the Linked Triangles Problem
(Update 2/22/2023, 6/9/2023) Alternative Solutions
Here is another Quantum math magazine Brainteaser.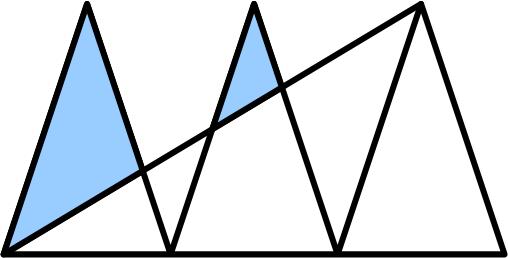
“Two wheels roll toward each other with identical angular velocity. At the moment of collision they contact each other at the same points that touched the ground before they began rolling. Could the radii of the wheels differ?”
See the Rolling Wheels Puzzle for solution.
This is a nice little puzzle from the late Nick Berry’s Datagenetics Blog.
“A quick little puzzle this week. (I tried to track down the original source, but reached a dead-end with a web search as the site that hosted it, a blogspot page under the name fivetriangles appears password protected, and no longer maintained). …
There are three identical triangles with aligned bases (in the original problem, it is stated they are equilateral, but I don’t think that really matters; Any congruent triangles will do, and I’m going to use isosceles triangles in my solving). If we say that one triangle has the area A, what is the area of the two shaded regions?”
See the Three Triangles Puzzle for solutions.
