 One of the all-time examples of chance intervening in history is Christopher Columbus’s putative discovery of America. Moreover, the legend of this discovery is filled with erroneous information that was traditionally foisted upon unsuspecting elementary school children. One of the most egregious errors was the assertion that Columbus was trying to prove the earth was round and not flat. I had a picture book when I was young that showed sailors tumbling off the edge of a flat earth.
One of the all-time examples of chance intervening in history is Christopher Columbus’s putative discovery of America. Moreover, the legend of this discovery is filled with erroneous information that was traditionally foisted upon unsuspecting elementary school children. One of the most egregious errors was the assertion that Columbus was trying to prove the earth was round and not flat. I had a picture book when I was young that showed sailors tumbling off the edge of a flat earth.
I first came upon the demythologizing of the Columbus legend from reading Isaac Azimov’s anthologized 1962 column “The Shape of Things”. His tale is so well-written, that I want to include it in its entirety. I have augmented it with some more detailed footnotes and illustrations.

 This essay introduces a topic I have been thinking about for a number of years. It also may allow me to connect the math impulse to a wider range of thoughts than just those based on math or even science.
This essay introduces a topic I have been thinking about for a number of years. It also may allow me to connect the math impulse to a wider range of thoughts than just those based on math or even science.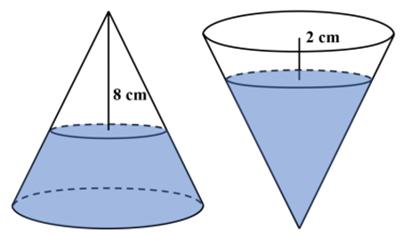 I was astonished that this problem was suitable for 8th graders. First of all the formula for the volume of a cone is one of the least-remembered of formulas, and I certainly never remember it. So my only viable approach was calculus, which is probably not a suitable solution for an 8th grader.
I was astonished that this problem was suitable for 8th graders. First of all the formula for the volume of a cone is one of the least-remembered of formulas, and I certainly never remember it. So my only viable approach was calculus, which is probably not a suitable solution for an 8th grader.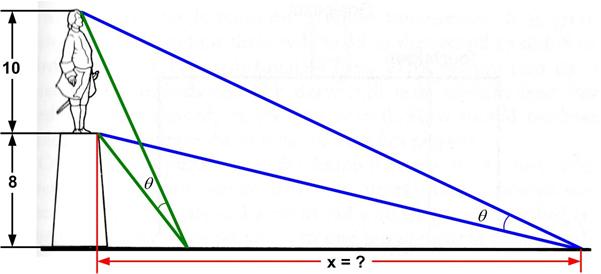 This is an old problem I had seen before. Here is David Wells’s rendition:
This is an old problem I had seen before. Here is David Wells’s rendition: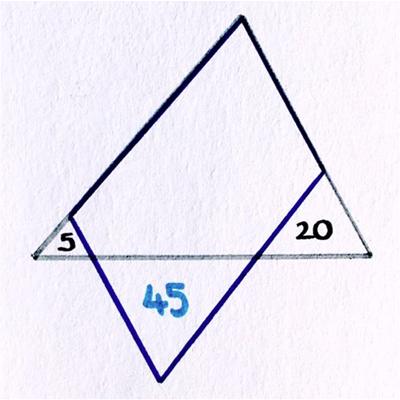
 A mathematics friend of mine just sent me this link to a 2017
A mathematics friend of mine just sent me this link to a 2017 
 Futility Closet presented a nifty method of solving the “counterfeit coin in 12 coins” problem in a way I had not seen before by mapping the problem into numbers in base 3. It wasn’t immediately clear to me how their solution worked, so I decided to write up my own explanation.
Futility Closet presented a nifty method of solving the “counterfeit coin in 12 coins” problem in a way I had not seen before by mapping the problem into numbers in base 3. It wasn’t immediately clear to me how their solution worked, so I decided to write up my own explanation.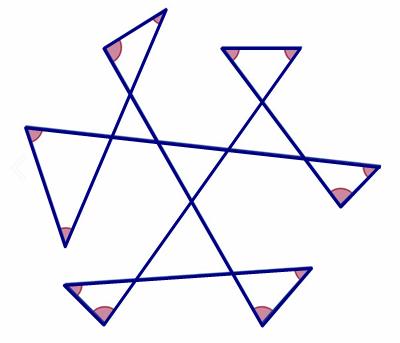
 Setting aside my chagrin that the following problem was given to pre-university students, I initially found the problem to be among the daunting ones that offer little information for a solution. It also was a bit “inelegant” to my way of thinking, since it involved considering some separate cases. Still, the end result turned out to be unique and satisfying (Talwalkar’s Note 2 was essential for a unique solution, since the problem as stated was ambiguous).
Setting aside my chagrin that the following problem was given to pre-university students, I initially found the problem to be among the daunting ones that offer little information for a solution. It also was a bit “inelegant” to my way of thinking, since it involved considering some separate cases. Still, the end result turned out to be unique and satisfying (Talwalkar’s Note 2 was essential for a unique solution, since the problem as stated was ambiguous).