Author Archives: Jim Stevenson

Marching Cadets and Dog Problem

In my search for new problems I came across this one from Martin Gardner:

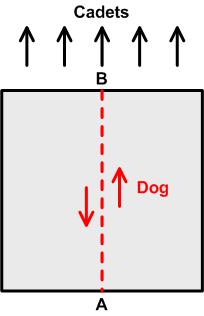
“A square formation of Army cadets, 50 feet on the side, is marching forward at a constant pace [see Figure]. The company mascot, a small terrier, starts at the center of the rear rank [position A in the illustration], trots forward in a straight line to the center of the front rank [position B], then trots back again in a straight line to the center of the rear. At the instant he returns to position A, the cadets have advanced exactly 50 feet. Assuming that the dog trots at a constant speed and loses no time in turning, how many feet does he travel?”

Gardner gives a follow-up problem that is virtually impossible:

“If you solve this problem, which calls for no more than a knowledge of elementary algebra, you may wish to tackle a much more difficult version proposed by the famous puzzlist Sam Loyd. Instead of moving forward and back through the marching cadets, the mascot trots with constant speed around the outside of the square, keeping as close as possible to the square at all times. (For the problem we assume that he trots along the perimeter of the square.) As before, the formation has marched 50 feet by the time the dog returns to point A. How long is the dog’s path?”

Answer.

See the Marching Cadets and Dog Problem for solutions.

Alberti’s Perspective Construction

I was reading yet another book on the Scientific Revolution when I came across a discussion of the mathematical significance of the invention of perspective for painting in the 15th century Italian Renaissance. The main player in the saga was Leon Battista Alberti (1404 – 1472) and his tome De Pictura (On Painting) (1435-6), which contained the first mathematical presentation of perspective. Even though mathematics was advertised, it was not at the level of trigonometry I used in my post “The Perspective Map”, but rather entailed simple Euclidean plane geometry. So the discussion was largely historical rather than mathematical. Nevertheless, I became curious to learn how much Alberti was able to discover about perspective without a lot of math. This essay is the result.

See Alberti’s Perspective Construction

(Update 7/29/2019)  I got a response! Continue reading →

Star Polygon Problem

This is problem #25 from the UKMT 2014 Senior Challenge.

“Figure 1 shows a tile in the form of a trapezium [trapezoid], where a = 83⅓°. Several copies of the tile placed together form a symmetrical pattern, part of which is shown in Figure 2. The outer border of the complete pattern is a regular ‘star polygon’. Figure 3 shows an example of a regular ‘star polygon’.
How many tiles are there in the complete pattern?
_____A_48_____B_54_____C_60_____D_66_____E_72”

Answer.

See the Star Polygon Problem for solutions.

Mr. Gubbins in a Fog

This is another delightful H. E. Dudeney puzzle.

“Mr. Gubbins, a diligent man of business, was much inconvenienced by a London fog. The electric light happened to be out of order and he had to manage as best he could with two candles. His clerk assured him that though both were of the same length one candle would burn for four hours and the other for five hours. After he had been working some time he put the candles out as the fog had lifted, and he then noticed that what remained of one candle was exactly four times the length of what was left of the other.

When he got home that night Mr. Gubbins, who liked a good puzzle, said to himself, ‘Of course it is possible to work out just how long those two candles were burning to-day. I’ll have a shot at it.’ But he soon found himself in a worse fog than the atmospheric one. Could you have assisted him in his dilemma? How long were the candles burning?”

Answer.

See Mr. Gubbins in a Fog for a solution.

Cube Roots Problem

In a June Chalkdust book review of Daniel Griller’s second book, Problem solving in GCSE mathematics, Matthew Scroggs presented the following problem #65 from the book (without a solution):
“Solve _______________”

Scroggs’s initial reaction to the problem was “it took me a while to realise that I even knew how to solve it.”

Mind you, according to Wikipedia, “GCSEs [General Certificate of Secondary Education] were introduced in 1988 [in the UK] to establish a national qualification for those who decided to leave school at 16, without pursuing further academic study towards qualifications such as A-Levels or university degrees.” My personal feeling is that any student who could solve this problem should be encouraged to continue their education with a possible major in a STEM field.

Answer.

See Cube Roots Problem for a solution.

A Mathematician in the Jury Box

This is a great posting by the mathematician James Propp on his website Mathematical Enchantments, not only for the main story about his experience as a mathematician at a trial, but also for his short excursion into the idea of definitions in mathematics—basically the same topic I was trying to address in my posts on “A Meditation on ‘Is’ in Mathematics” here and here.

Normally I would excerpt such an article and provide the link to the full article, but given the short half-life of links I have also provided a full PDF copy just in case. You should visit the link to see the comments, which I have not included (Propp is lucky to have some of those). In fact, you should take the opportunity to peruse a number of his articles, if you have not already, which are longer in nature, appear monthly, and provide some great insights into mathematics (his pseudosphere icon is the Beltrami surface, which he discusses elsewhere).

See A Mathematician in the Jury Box.

Rising Sun

Here is a problem from the UKMT Senior (17-18 year-old) Mathematics Challenge for 2012:

“A semicircle of radius r is drawn with centre V and diameter UW. The line UW is then extended to the point X, such that UW and WX are of equal length. An arc of the circle with centre X and radius 4r is then drawn so that the line XY is tangent to the semicircle at Z, as shown. What, in terms of r, is the area of triangle YVW?”

Answer.

See the Rising Sun for solutions.

  1. Pages:
  3. 1
  4. ...
  5. 33
  6. 34
  7. 35
  8. 36
  9. 37
  10. 38
  11. 39
  12. ...
  13. 47