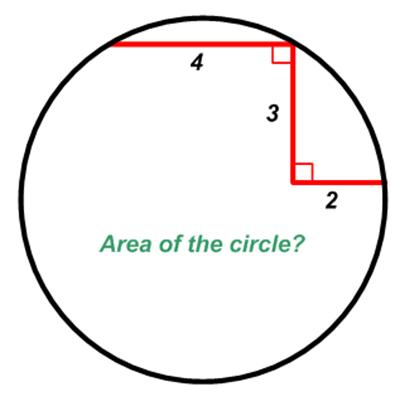
 This is a straight-forward problem from Osdinato on Twitter in 2018.
This is a straight-forward problem from Osdinato on Twitter in 2018.
“Find the area of the circle in the figure.”
See Circle-Step Puzzle for a solution.

 This is a straight-forward problem from Osdinato on Twitter in 2018.
This is a straight-forward problem from Osdinato on Twitter in 2018.
“Find the area of the circle in the figure.”
See Circle-Step Puzzle for a solution.
 This is another problem from Dan Griller.
This is another problem from Dan Griller.
“In the triangle ABC, CN and MB are straight lines, ÐCAB = 90° and CM = MA = AN = NB = 5. Find the exact area of the shaded region.”
See the Triangle Bow-tie Problem for a solution.
 I think this turned out to be an even trickier problem than Alex Bellos thought.
I think this turned out to be an even trickier problem than Alex Bellos thought.
“Tricky triangle This one was sent in by a reader, aged 85, who first saw it in 1960. He is a roboticist who passed through Harvard, Princeton, Stanford and IBM. He says it is his favourite puzzle. ‘I’ve given this puzzle to perhaps 100 people. Over 80% have no idea how to solve it.’ What is the length of AD, the dashed line?”
See Tricky Triangle for solutions.
 This is another puzzle from BL’s Weekly Math Games.
This is another puzzle from BL’s Weekly Math Games.
“a + b + c = 2, and
a2 + b2 + c2 = 12
where a, b, and c are real numbers. What is the difference between the maximum and minimum possible values of c?”
The original problem statement mentioned a fourth real number d, but I considered it a typo, since it was not involved in the problem.
See Sphere and Plane Puzzle for a solution.
 This is an interesting problem from the collection Five Hundred Mathematical Challenges.
This is an interesting problem from the collection Five Hundred Mathematical Challenges.
“Problem 251. Let ABCD be a square, F be the midpoint of DC, and E be any point on AB such that AE > EB. Determine N on BC such that DE || FN. Prove that EN is tangent to the inscribed circle of the square.”
See the Parallel Lines Problem.
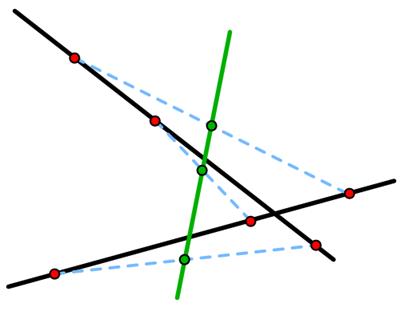 I came across this remarkable result in Futility Closet:
I came across this remarkable result in Futility Closet:
“On each of these two black lines is a trio of red points marked by the same distances. The midpoints of segments drawn between corresponding points are collinear.
(Discovered by Danish mathematician Johannes Hjelmslev.)”
This result seems amazing and mysterious. I wondered if I could think of a proof. I found a simple approach that did not use plane geometry. And suddenly, like a magic trick exposed, the result seemed obvious.
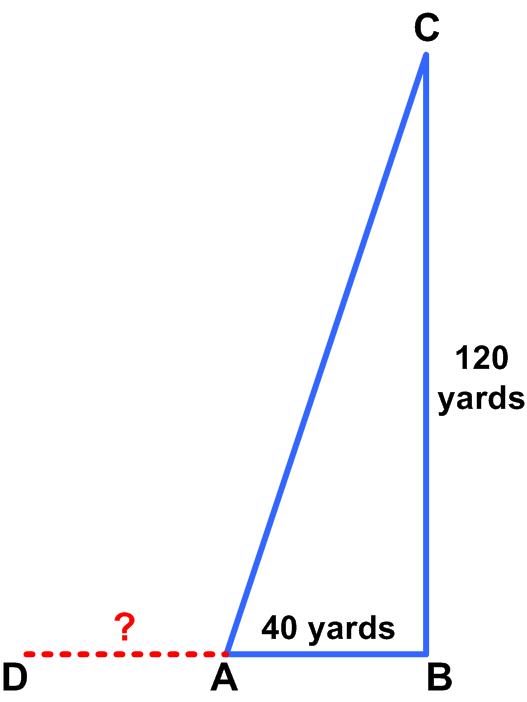 The following puzzle is from the Irishman Owen O’Shea.
The following puzzle is from the Irishman Owen O’Shea.
“The figure shows the location of three flags [at A, B, and C] in one of the fields on a neighbor’s farm. The angle ABC is a right angle. Flag A is 40 yards from Flag B. Flag B is 120 yards from flag C. Thus, if one was to walk from A to B and then on to C, one would walk a total of 160 yards.
Now there is a point, marked by flag D, [directly] to the left of flag A. Curiously, if one were to walk from flag A to flag D and then diagonally across to flag C, one would walk a total distance of 160 yards.
The question for our puzzlers is this: how far is it from flag D to flag A?”
This problem has a simple solution. But it also suggests a more advanced alternative approach.
See the Distance to Flag Problem for a solution.
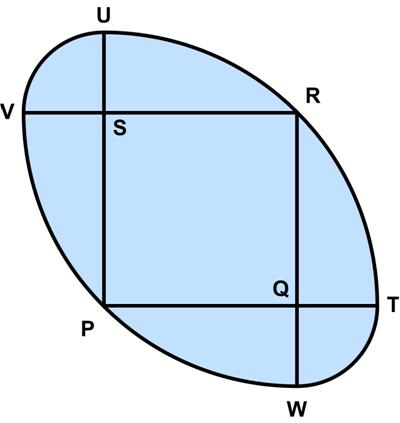 Here is another UKMT Senior Challenge problem for 2017.
Here is another UKMT Senior Challenge problem for 2017.
“The diagram shows a square PQRS with edges of length 1, and four arcs, each of which is a quarter of a circle. Arc TRU has centre P; arc VPW has centre R; arc UV has centre S; and arc WT has centre Q.
What is the length of the perimeter of the shaded region?
A_6___B_(2√2 – 1)π___C_(√2 – 1/2)π ___D_2___E_(3√2 – 2)π”
See Elliptic Circles for a solution.
 Since the changes in Twitter (now X), I have not been able to see the posts, not being a subscriber. But I noticed poking around that some twitter accounts were still viewable. However, like some demented aging octogenarian they had lost track of time, that is, instead of being sorted with the most recent post first, they showed a random scattering of posts from different times. So a current post could be right next to one several years ago. That is what I discovered with the now defunct MathsMonday site. I found a post from 10 May 2021 that I had not seen before, namely,
Since the changes in Twitter (now X), I have not been able to see the posts, not being a subscriber. But I noticed poking around that some twitter accounts were still viewable. However, like some demented aging octogenarian they had lost track of time, that is, instead of being sorted with the most recent post first, they showed a random scattering of posts from different times. So a current post could be right next to one several years ago. That is what I discovered with the now defunct MathsMonday site. I found a post from 10 May 2021 that I had not seen before, namely,
“The points A and B are on the curve y = x2 such that AOB is a right angle. What points A and B will give the smallest possible area for the triangle AOB?”
See the Pythagorean Parabola Puzzle for solution.
(Update 9/1/2023) Elegant Alternative Solution by Oscar Rojas
Continue reading
 The Futility Closet website had the following problem:
The Futility Closet website had the following problem:
“In isosceles triangle ABC, CD = AB and BE is perpendicular to AC. Show that CEB is a 3-4-5 right triangle.”
See a Triangle Puzzle