
Here is a mind-numbing logic puzzle from Futility Closet.
“A puzzle by H.A. Thurston, from the April 1947 issue of Eureka, the journal of recreational mathematics published at Cambridge University:
Five people make the following statements:—

Which of these statements are true and which false? It will be found on trial that there is only one possibility. Thus, prove or disprove Fermat’s last theorem.”
Normally I would forgo something this complicated, but I thought I would give it a try. I was surprised that I was able to solve it, though it took some tedious work. (Hint: truth tables. See the “Pointing Fingers” post regarding truth tables.)
One important note. The author is a bit cavalier about the use of “Either …, or …”. In common parlance this means “either P is true or Q is true, but not both” (exclusive “or”: XOR), whereas in logic “or” means “either P is true or Q is true, or possibly both” (inclusive “or”: OR). I assumed all “Either …, or …” and “or” expressions were the logical inclusive “or”, which turned out to be the case.
See the Fermat’s Last Theorem Puzzle

 This is another fairly simple puzzle from Futility Closet from a while ago (2014).
This is another fairly simple puzzle from Futility Closet from a while ago (2014). Futility Closet has another
Futility Closet has another  Here is a seemingly simple problem from Futility Closet.
Here is a seemingly simple problem from Futility Closet.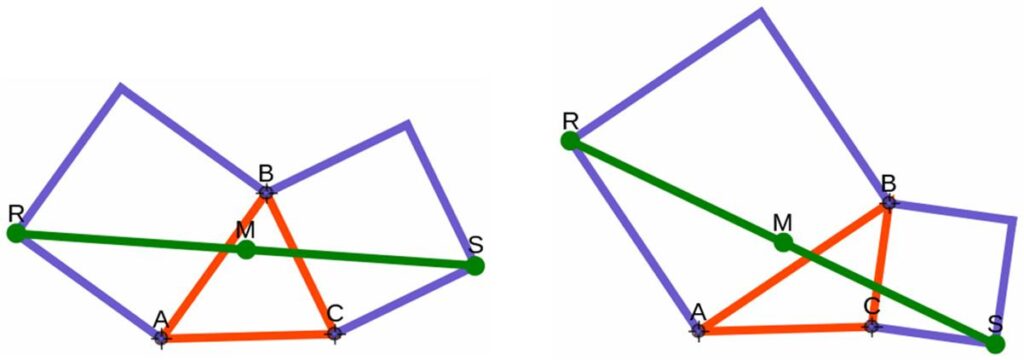
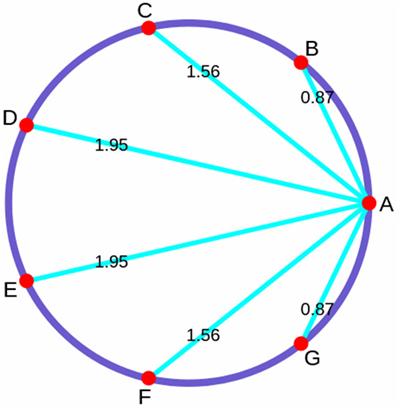 Futility Closet
Futility Closet Here is a simple problem from an old
Here is a simple problem from an old 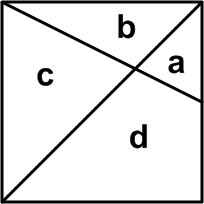 Here is a simple Futility Closet problem from 2014.
Here is a simple Futility Closet problem from 2014. Here is a nice logic puzzle from 2014 Futility Closet.
Here is a nice logic puzzle from 2014 Futility Closet.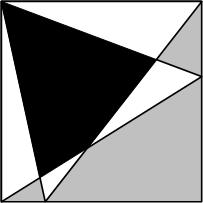 This is a problem from a while back (2015) at Futility Closet.
This is a problem from a while back (2015) at Futility Closet.