 This is a simple problem from Five Hundred Mathematical Challenges:
This is a simple problem from Five Hundred Mathematical Challenges:
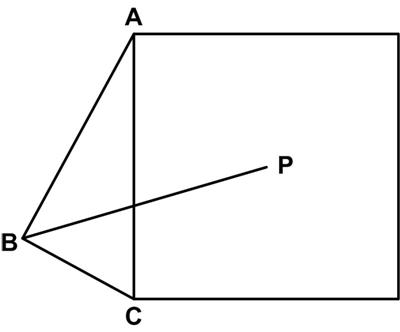
“Problem 24. Let P be the center of the square constructed on the hypotenuse AC of the right-angled triangle ABC. Prove that BP bisects angle ABC.”
See the Center of Square Problem

 This is a simple problem from Five Hundred Mathematical Challenges:
This is a simple problem from Five Hundred Mathematical Challenges:
“Problem 24. Let P be the center of the square constructed on the hypotenuse AC of the right-angled triangle ABC. Prove that BP bisects angle ABC.”
See the Center of Square Problem
 Here is another, more challenging, problem from the Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos).
Here is another, more challenging, problem from the Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos).
“An event that occurred during The Adventure of the Wandering Bishops inspired Holmes to devise a particularly tricky little mental exercise for my ongoing improvement. There were times when I thoroughly appreciated and enjoyed his efforts, and times when I found them somewhat unwelcome. I’m afraid that this was one of the latter occasions. It had been a bad week.
‘Picture three farmers,’ Holmes told me. ‘Hooklanders. We’ll call them Ern, Ted, and Hob.’
‘If I must,’ I muttered.
‘It will help,’ Holmes replied. ‘Ern has a horse and cart, with an average speed of eight mph. Ted can walk just one mph, given his bad knee, and Hob is a little better at two mph, thanks to his back.’
‘A fine shower,’ I said. ‘Can’t I imagine them somewhat fitter?’
‘Together, these worthies want to go from Old Hook to Coreham, a journey of 40 miles. So Ern got Ted in his cart, drove him most of the way, and dropped him off to walk the rest. Then he went back to get Hob [who was still walking], and took him into Coreham, arriving exactly as Ted did. How long did the journey take?’
Can you find a solution?”
I added the statement in brackets. I initially thought Hob waited in Old Hook until Ted fetched him. But the solution indicated that was not the case. So I realized Hob had started out at the same time as the others. The solution has some hairy arithmetic. Even knowing the answer it is difficult to do the computations without a mistake.
See the Old Hook Puzzle for solutions.
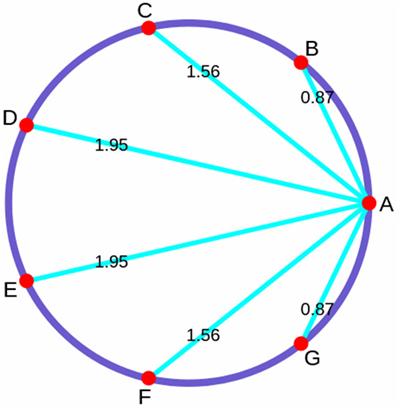 Futility Closet describes a result that is startling, amazing, and mysterious.
Futility Closet describes a result that is startling, amazing, and mysterious.
“This is pretty: If you choose n > 1 equally spaced points on a unit circle and connect one of them to each of the others, the product of the lengths of these chords equals n.”
The Futility Closet posting includes an interactive display using Wolfram Technology by Jay Warendorff that let’s you select different n and see the results. It also includes a reference to a paper that proves the result; only the paper uses residue theory from complex variables, which seems a bit over-kill, though slick, for such a problem. I found a simpler route.
 The “Moving Up” post recalled an unforgettable moment in my past, when I still rode the Washington Metro somewhat sporadically (my youth was spent riding busses, before the advent of the Metro). It was the first time I confronted the escalator at the DuPont Circle stop. I was going to a math talk with a friend and we were busy discussing math when I stepped onto the escalator. Suddenly, I looked up and saw the stairs disappearing 188 feet into the heavens and froze. I have always been afraid of heights, and the escalator brought out all the customary terror. There was of course no turning back. And then people started bolting up the stairs past me, not always avoiding brushing by.
The “Moving Up” post recalled an unforgettable moment in my past, when I still rode the Washington Metro somewhat sporadically (my youth was spent riding busses, before the advent of the Metro). It was the first time I confronted the escalator at the DuPont Circle stop. I was going to a math talk with a friend and we were busy discussing math when I stepped onto the escalator. Suddenly, I looked up and saw the stairs disappearing 188 feet into the heavens and froze. I have always been afraid of heights, and the escalator brought out all the customary terror. There was of course no turning back. And then people started bolting up the stairs past me, not always avoiding brushing by.
My hand was clamped to the handrail in a death grip. I had to hold on even tighter as the sweat of fear made my hands slippery. In such situations I often feel a sense of vertigo or loss of balance. It was then that I thought the handrail was moving faster than the steps so that I was being pulled forward. I couldn’t tell if it was the vertigo or an actual movement. In any case, I periodically let go and repositioned my death grip. After an eternity, it was over, and I staggered out into the street. Needless to say, on our return I sought out the elevator. Fortunately, it was working—not always the case in the Washington Metro.
Once my brain was functioning a bit, I pondered the question of the relative speeds of the handrail and steps. How could they be synchronized? But after a while I left it as an interesting curiosity.
(Update 9/13/2025) The Railing Does Move Faster Continue reading
 Here is a simple problem from an old Futility Closet posting.
Here is a simple problem from an old Futility Closet posting.
“My wife and I walk up an ascending escalator. I climb 20 steps and reach the top in 60 seconds. My wife climbs 16 steps and reaches the top in 72 seconds. If the escalator broke tomorrow, how many steps would we have to climb?”
See Moving Up for solutions.
 This typical problem from the prolific H. E. Dudeney may be a bit tricky at first.
This typical problem from the prolific H. E. Dudeney may be a bit tricky at first.
“104.—CATCHING THE THIEF.
“Now, constable,” said the defendant’s counsel in cross-examination,” you say that the prisoner was exactly twenty-seven steps ahead of you when you started to run after him?”
“Yes, sir.”
“And you swear that he takes eight steps to your five?”
“That is so.”
“Then I ask you, constable, as an intelligent man, to explain how you ever caught him, if that is the case?”
“Well, you see, I have got a longer stride. In fact, two of my steps are equal in length to five of the prisoner’s. If you work it out, you will find that the number of steps I required would bring me exactly to the spot where I captured him.”
Here the foreman of the jury asked for a few minutes to figure out the number of steps the constable must have taken. Can you also say how many steps the officer needed to catch the thief?”
See Catching the Thief for solutions.
 Here is yet another collection of beautiful geometric problems from Catriona Agg (née Shearer). For some reason I found these a bit more challenging than the previous ones. Some of them required more time to “see” the breakthrough.
Here is yet another collection of beautiful geometric problems from Catriona Agg (née Shearer). For some reason I found these a bit more challenging than the previous ones. Some of them required more time to “see” the breakthrough.
See Geometric Puzzle Magnificence (revised)
(Update 11/13/2022) Problem #3 Solution Corrected Continue reading
 Here is another challenging problem from the first issue of the 1874 The Analyst, which also appears in Benjamin Wardhaugh’s book.
Here is another challenging problem from the first issue of the 1874 The Analyst, which also appears in Benjamin Wardhaugh’s book.
“3. If a line make an angle of 40° with a fixed plane, and a plane embracing this line be perpendicular to the fixed plane, how many degrees from its first position must the plane embracing the line revolve in order that it may make an angle of 45° with the fixed plane?
—Communicated by Prof. A. Schuyler, Berea, Ohio.”
Part of the challenge is to construct a diagram of the problem. I used techniques for a solution that were barely in use when this problem was posed in 1874. The contrast between then and now is most revealing.
See the Rotating Plane Problem for solutions.
 Here is a challenging problem from the 1874 The Analyst.
Here is a challenging problem from the 1874 The Analyst.
“A cask containing a gallons of wine stands on another containing a gallons of water; they are connected by a pipe through which, when open, the wine can escape into the lower cask at the rate of c gallons per minute, and through a pipe in the lower cask the mixture can escape at the same rate; also, water can be let in through a pipe on the top of the upper cask at a like rate. If all the pipes be opened at the same instant, how much wine will be in the lower cask at the end of t minutes, supposing the fluids to mingle perfectly?
— Communicated by Artemas Martin, Mathematical Editor of Schoolday Magazine, Erie, Pennsylvania.”
I found the problem in Benjamin Wardhaugh’s book where he describes The Analyst:
“Beginning in 1874 and continuing as Annals of Mathematics from 1884 onward, The Analyst appeared monthly, published in Des Moines, Iowa, and was intended as “a suitable medium of communication between a large class of investigators and students in science, comprising the various grades from the students in our high schools and colleges to the college professor.” It carried a range of mathematical articles, both pure and applied, and a regular series of mathematical problems of varying difficulty: on the whole they seem harder than those in The Ladies’ Diary and possibly easier than the Mathematical Challenges in the extract after the next. Those given here appeared in the very first issue.”
I tailored my solution after the “Diluted Wine Puzzle”, though this problem was more complicated. Moreover, the final solution must pass from discreet steps to continuous ones.
There is a bonus problem in a later issue:
“19. Referring to Question 4, (No. 1): At what time will the lower cask contain the greatest quantity of wine?
—Communicated by Prof. Geo. R. Perkins.”
See the Wine Into Water Problem for solutions.
 This is another Brainteaser from the Quantum math magazine .
This is another Brainteaser from the Quantum math magazine .
“How can a polygonal line BDEFG be drawn in a triangle ABC so that the five triangles obtained have the same area?”
I found this problem rather challenging, especially when I first tried to solve it analytically (using hyperbolas). Eventually I arrived at a procedure that would accomplish the result. (revised)
See the Equitable Slice Problem (revised)
(Update 9/22/2021) I goofed. I erroneously and foolishly thought Quantum had not solved the problem. Upon a closer reading I see what they were getting at and revised the posting.