This is a slightly different mystery number puzzle from the December 2023 MathsJam Shout. It provides a simpler puzzle as a respite from the more challenging problems.
Category Archives: Puzzles and Problems
Two Containers Mixing Puzzle
This is a slightly different type of a mixture problem from Dan Griller.
“Two containers A and B sit on a table, partially filled with water. First, 40% of the water in A is poured into B, which completely fills it. Then 75% of the water in B is poured into A, which completely fills it. 80% of the water in A is poured into B, which completely fills it. Calculate the ratio of the capacity of container A to the capacity of container B, and the fraction of container A that was occupied by water at the start.”
See the Two Containers Mixing Puzzle for solution.
Yet Another Race
This is another race puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings for 2013.
“In a 100 meter race, Jacob can beat Johann by 5 meters, and Johann can beat Nicolaus by 10 meters. By how much can Jacob beat Nicolaus?”
See Yet Another Race for a solution.
Circles in Circles
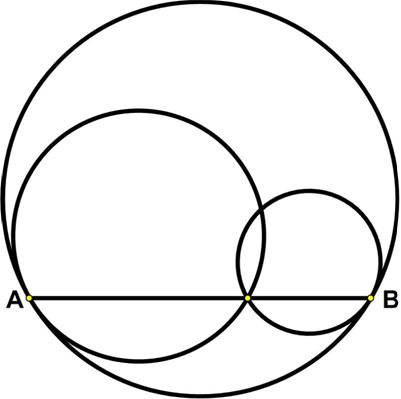Here is another problem from the “Challenges” section of the Quantum magazine.
“Inside a circle there are two intersecting circles. One of them touches the big circle in point A, the other in point B. Prove that if segment AB meets the smaller circles at one of their common points, then the sum of their radii equals the radius of the big circle. Is the converse true? (A. Vesyolov)”
Maximized Box Problem
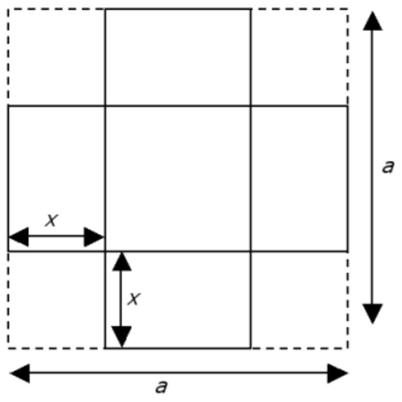This problem is from Colin Hughes’s Maths Challenge website (mathschallenge.net).
“Four corners measuring x by x are removed from a sheet of material that measures a by a to make a square based open-top box. Prove that the volume of the box is maximised iff the area of the base is equal to the area of the four sides.”
See the Maximized Box Problem
Two More Jugs
Here is another classic example of the three jug problem posed in the Mathigon Puzzle Calendars for 2017.
“How can I measure exactly 8 liters of water, using just one 11 liter and one 6 liter bucket?”
It is assumed you have unlimited access to water (the “third jug” of at least 17 liters). You can only fill or empty the jugs, unless in poring from one jug to another you fill the receiving jug before emptying the poring jug. (Hint: see the Three Jugs Problem.)
See Two More Jugs.
Elliptical Medians Problem
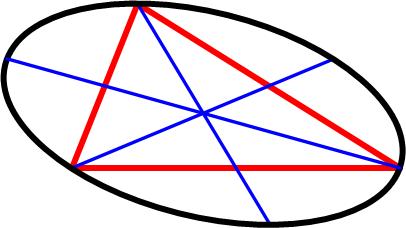This is a tantalizing problem from the 1977 Crux Mathematicorum.
“278. Proposed by W.A. McWorter, Jr., The Ohio State University.
If each of the medians of a triangle is extended beyond the sides of the triangle to 4/3 its length, show that the three new points formed and the vertices of the triangle all lie on an ellipse.”
See the Elliptical Medians Problem
Storm Chaser Problem
This is a somewhat challenging problem from the 1997 American Invitational Mathematics Exam (AIME).
“A car travels due east at 2/3 miles per minute on a long, straight road. At the same time, a circular storm, whose radius is 51 miles, moves southeast at √2/2 miles per minute. At time t = 0, the center of the storm is 110 miles due north of the car. At time t = t1 minutes, the car enters the storm circle, and at time t = t2 minutes, the car leaves the storm circle. Find (t1 + t2)/2.”
See the Storm Chaser Problem for solutions.
String of Beads Puzzle
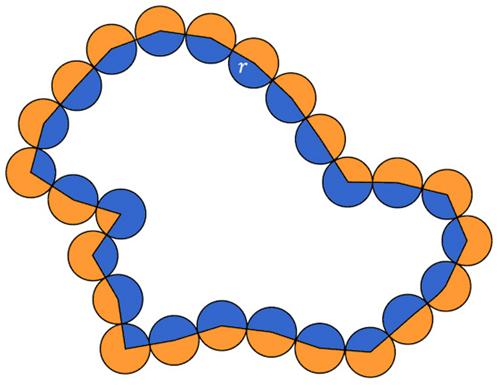This is a nifty problem from Presh Talwalkar.
“This is from a Manga called Q.E.D. I thank Sparky from the Philippines for the suggestion!
A string of beads is formed from 25 circles of the same size. The string passes through the center of each circle. The area enclosed by the string inside each circle is shaded in blue, and the remaining areas of the circles are shaded in orange. What is the value of the orange area minus the blue area? Calculate the area in terms of r, the radius of each circle.”
See the String of Beads Puzzle for solutions.
After Five O’clock
This is a fairly extensive clock problem by Geoffrey Mott-Smith from 1954.
“The clock shown in the illustration has just struck five. A number of things are going to happen in this next hour, and I am curious to know the exact times.
- At what time will the two hands coincide?
- At what time will the two hands first stand at right angles to each other?
- At one point the hands will stand at an angle of 30 degrees, the minute hand being before the hour hand. Then the former will pass the latter and presently make an angle of 60 degrees on the other side. How much time will elapse between these two events?”
See After Five O’Clock for solutions.