This is a straight-forward problem by Geoffrey Mott-Smith from 1954.
“Three tangent circles of equal radius r are drawn, all centers being on the line OE. From O, the outer intersection of this axis with the left-hand circle, line OD is drawn tangent to the right-hand circle. What is the length, in terms of r, of AB, the segment of this tangent which forms a chord in the middle circle?”
See An Intercept Problem for solutions.
This is another candle burning problem, presented by Presh Talwalkar.
“Two candles of equal heights but different thicknesses are lit. The first burns off in 8 hours and the second in 10 hours. How long after lighting, in hours, will the first candle be half the height of the second candle? The candles are lit simultaneously and each burns at a constant linear rate.”
See Two Candles for solutions.
Here is yet another (belated) collection of beautiful geometric problems from Catriona Agg (née Shearer).
This problem comes from the Scottish Mathematical Council (SMC) Senior Mathematical Challenge of 2007:
“A group of seven girls—Ally, Bev, Chi-chi, Des, Evie, Fi and Grunt—were playing a game in which the counters were beans. Whenever a girl lost a game, from her pile of beans she had to give each of the other girls as many beans as they already had. They had been playing for some time and they all had different numbers of beans. They then had a run of seven games in which each girl lost a game in turn, in the order given above. At the end of this sequence of games, amazingly, they all had the same number of beans—128. How many did each of them have at the start of this sequence of seven games?”
See the Seven Girls Puzzle for solutions.
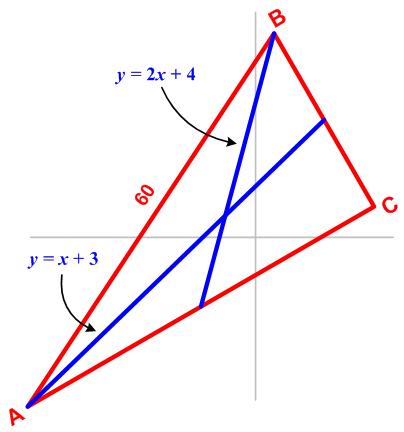This is a challenging problem from the 1986 American Invitational Mathematics Exam (AIME).
“Let triangle ABC be a right triangle in the xy-plane with a right angle at C. Given that the length of the hypotenuse AB is 60, and that the medians through A and B lie along the lines y = x + 3 and y = 2x + 4 respectively, find the area of triangle ABC.”
I have included a sketch to indicate that the sides of the right triangle are not parallel to the Cartesian coordinate axes.
The AIME (American Invitational Mathematics Examination) is an intermediate examination between the American Mathematics Competitions AMC 10 or AMC 12 and the USAMO (United States of America Mathematical Olympiad). All students who took the AMC 12 (high school 12th grade) and achieved a score of 100 or more out of a possible 150 or were in the top 5% are invited to take the AIME. All students who took the AMC 10 (high school 10th grade and below) and had a score of 120 or more out of a possible 150, or were in the top 2.5% also qualify for the AIME.
See the Challenging Triangle Problem for solutions.
Here is another elegant Quantum math magazine Brainteaser from the imaginative V. Proizvolov.
“Two isosceles right triangles are placed one on the other so that the vertices of each of their right angles lie on the hypotenuse of the other triangle (see the figure at left). Their other four vertices form a quadrilateral. Prove that its area is divided in half by the segment joining the right angles. (V. Proizvolov)”
Here is another logic problem from Ian Stewart.
Therefore:
No cat with blunt claws will play with a gorilla.
Is the deduction logically correct?
I confess I don’t know what a heron suit is. Google showed various garments with herons imprinted on the cloth, so maybe that is what it is.
See the Heron Suit Problem for a solution.
This is a most interesting problem proposed by Mirangu and retweeted by Catriona Agg:
“Two equilateral triangles share a vertex. What is the proportion red : green?”
See the Two Equilateral Triangles for solutions.
This is a thoughtful puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings.
“A ladder is leaning against a wall. The base of the ladder starts sliding away from the wall, with the top of the ladder sliding down the wall. As the ladder slides, you watch the red point in the middle of the ladder. What figure does the red point trace? What about other points on the ladder?”
See the Ladder Locus Puzzle for solutions.
Here is another problem from the Polish Mathematical Olympiads published in 1960.
“95. In a parallelogram of given area S each vertex has been connected with the mid-points of the opposite two sides. In this manner the parallelogram has been cut into parts, one of them being an octagon. Find the area of that octagon.”
See the Octagonal Area Problem for solutions.
