I came across this problem in Alfred Posamentier’s book, but I remember I had seen it a couple of places before and had never thought to solve it. At first, it seems like magic.

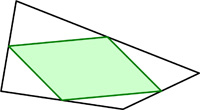
In any convex quadrilateral (line between any two points in the quadrilateral lies entirely inside the quadrilateral) inscribe a second convex quadrilateral with its vertices on the midpoints of the sides of the first quadrilateral. Show that the inscribed quadrilateral must be a parallelogram.

See the Magic Parallelogram.

(Update 5/15/2020) Matthew Scroggs has a different proof of the Magic Parallelogram for The Aperiodical’s Big Math Lockdown contest.