 This is a classic puzzle from Presh Talwalkar.
This is a classic puzzle from Presh Talwalkar.
“This puzzle has been asked as an interview question at tech companies like Google.
There are 100 lights numbered 1 to 100, all starting in the off position. There are also 100 people numbered 1 to 100. First, person 1 toggles every light switch (toggle means to change from off to on, or change from on to off). Then person 2 toggles every 2nd light switch, and so on, where person i toggles every ith light switch. The last person is person 100 who toggles every 100th switch.
After all 100 people have passed, which light bulbs will be turned on?”
I vaguely remembered the answer, which I confirmed after a few examples. But I didn’t remember an exact proof, so I thought I would give it a try.
Answer.
See 100 Light Bulbs Puzzle for solutions.
 This is a curious relation from the 2024 Math Calendar.
This is a curious relation from the 2024 Math Calendar.
 This is an old puzzle from Catriona Agg that I found on BL’s Math Games
This is an old puzzle from Catriona Agg that I found on BL’s Math Games 
 This is another problem from the c.100AD Chinese mathematical work, Jiǔ zhāng suàn shù (The Nine Chapters on the Mathematical Art) found at the MAA Convergence website Convergence.
This is another problem from the c.100AD Chinese mathematical work, Jiǔ zhāng suàn shù (The Nine Chapters on the Mathematical Art) found at the MAA Convergence website Convergence. This is an interesting problem from the 1966 Eureka magazine.
This is an interesting problem from the 1966 Eureka magazine. This is a classic
This is a classic 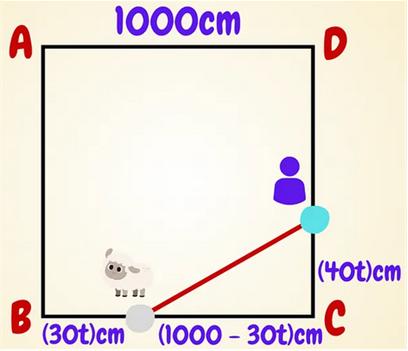 This is a slightly challenging
This is a slightly challenging  This is a
This is a  This is another nice problem from the 2025 Math Calendar.
This is another nice problem from the 2025 Math Calendar.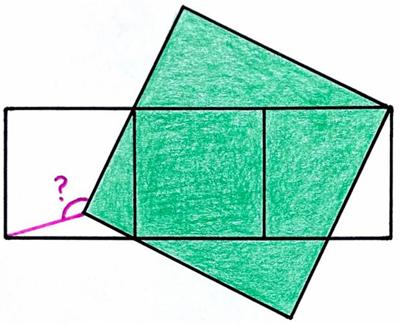 This is another Catriona Agg
This is another Catriona Agg