One of the books that has stuck with me over the years is Carl Becker’s The Declaration of Independence (1922, reprint 1942), not only for its incredibly clear and beautiful writing but also for its emphasis on the impact of the revolution most prominently caused by Isaac Newton, which was later subsumed under the term Scientific Revolution covering the entire 17th century. A consequence of this remarkable period was the so-called Enlightenment that followed in the 18th century and became the soil from which our nation’s founding ideas and documents sprang. Both these centuries have been further optimistically called the Age of Reason.
One of the books that has stuck with me over the years is Carl Becker’s The Declaration of Independence (1922, reprint 1942), not only for its incredibly clear and beautiful writing but also for its emphasis on the impact of the revolution most prominently caused by Isaac Newton, which was later subsumed under the term Scientific Revolution covering the entire 17th century. A consequence of this remarkable period was the so-called Enlightenment that followed in the 18th century and became the soil from which our nation’s founding ideas and documents sprang. Both these centuries have been further optimistically called the Age of Reason.
Our current times, awash in lies, corruption, and such terms as “alternative facts”, have been characterized as an assault on the rationalism and Enlightenment that shaped our founding. Any revisiting of these origins would seem to be a valuable endeavor to see if they still have validity. What makes Becker’s essay particularly relevant to me is the current pervasiveness of the mathematical view of reality that was launched by Newton some 300 years ago. Becker shows how this new way of thinking spread far beyond the bounds of mathematics and engendered a new “natural rights” philosophy that formed the foundation for the Declaration of Independence. Essentially the idea was that if the behavior of the natural world was based on (mathematical) laws, then so must the behavior of man be based on natural laws.
See Newton and Declaration of Independence
(Updates 10/31/2019, 9/18/2020, 3/9/2024) Steven Strogatz Confirmation, an Atlantic article, Natural Law

 It is a bit presumptuous to think I could reduce the universe of mathematics to some succinct essence, but ever since I first saw a column in Martin Gardner’s Scientific American Mathematical Games in 1967, I thought his example illustrated the essential feature of mathematics, or at least one of its principal attributes. And he posed it in a way that would be accessible to anyone. I especially wanted to credit Martin Gardner, since the idea resurfaced recently, uncredited, in some attractive videos by Katie Steckles and James Grime. (This reminds me of the Borges idea that “eighty years of oblivion are perhaps equal to novelty”.) See the
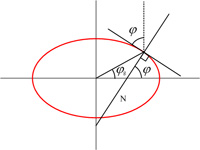
It is a bit presumptuous to think I could reduce the universe of mathematics to some succinct essence, but ever since I first saw a column in Martin Gardner’s Scientific American Mathematical Games in 1967, I thought his example illustrated the essential feature of mathematics, or at least one of its principal attributes. And he posed it in a way that would be accessible to anyone. I especially wanted to credit Martin Gardner, since the idea resurfaced recently, uncredited, in some attractive videos by Katie Steckles and James Grime. (This reminds me of the Borges idea that “eighty years of oblivion are perhaps equal to novelty”.) See the 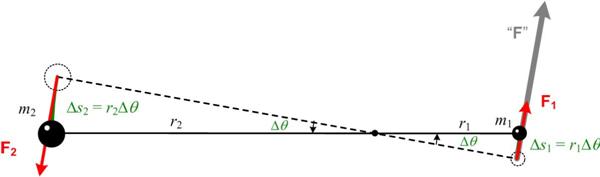 I have always had a tenuous relationship with the concept of angular momentum, but recently my concerns resurfaced when I did my studies on Kepler, and in particular his
I have always had a tenuous relationship with the concept of angular momentum, but recently my concerns resurfaced when I did my studies on Kepler, and in particular his 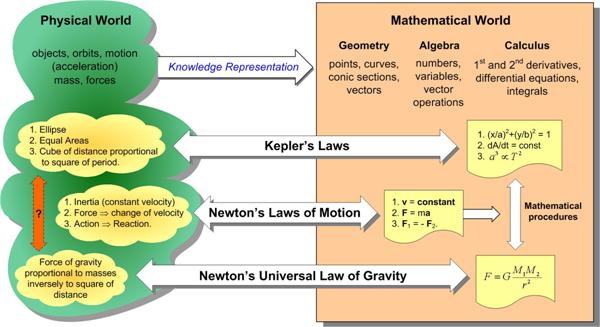 This post continues a meditation on the nature of mathematics begun in Part I. It involves the perennial question about whether mathematics is invented or discovered, and consequently evokes questions about mathematical reality. This subject is probably of little interest to most people, and even most mathematicians. But the extremely heavy involvement of mathematics in the descriptions of quantum mechanics, and the even more mathematically abstruse excursions into ideas such as string theory in an effort to wed quantum mechanics to general relativity, force us to confront the central place mathematics has in “explaining” our physical reality. Of course, this essay has no definitive answers, and leaves the situation as a mystery. See
This post continues a meditation on the nature of mathematics begun in Part I. It involves the perennial question about whether mathematics is invented or discovered, and consequently evokes questions about mathematical reality. This subject is probably of little interest to most people, and even most mathematicians. But the extremely heavy involvement of mathematics in the descriptions of quantum mechanics, and the even more mathematically abstruse excursions into ideas such as string theory in an effort to wed quantum mechanics to general relativity, force us to confront the central place mathematics has in “explaining” our physical reality. Of course, this essay has no definitive answers, and leaves the situation as a mystery. See 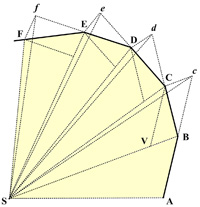 I have long been fascinated by Newton’s proof of Kepler’s Equal Areas Law and wanted to write about it. Of course, others have as well, but I wanted to emphasize an aspect of the proof that supported my philosophy of mathematics.
I have long been fascinated by Newton’s proof of Kepler’s Equal Areas Law and wanted to write about it. Of course, others have as well, but I wanted to emphasize an aspect of the proof that supported my philosophy of mathematics.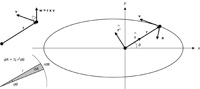 Years ago (1963) I got the paperback The Calculus:A Genetic Approach, by Otto Toeplitz, which presented the basic ideas of the differential and integral calculus from a historical point of view. One thing Toeplitz did at the end of his book that I had not seen in other texts was to show the equivalence of Kepler’s Laws and Newton’s Law of Gravity. (Since 1963 David Bressoud has developed this theme in his excellent 1991 text.) I thought I would try to emulate Toeplitz’s approach with more modern notation (vectors) and arguments in hopes of extracting the essential ideas from the clutter.
Years ago (1963) I got the paperback The Calculus:A Genetic Approach, by Otto Toeplitz, which presented the basic ideas of the differential and integral calculus from a historical point of view. One thing Toeplitz did at the end of his book that I had not seen in other texts was to show the equivalence of Kepler’s Laws and Newton’s Law of Gravity. (Since 1963 David Bressoud has developed this theme in his excellent 1991 text.) I thought I would try to emulate Toeplitz’s approach with more modern notation (vectors) and arguments in hopes of extracting the essential ideas from the clutter.