Here is a tricky little logarithm problem from the 2021 Math Calendar.
“Find x, where
log2(log4(x)) = log4(log2(x))”
As before, recall that all the answers are integer days of the month.
See Log Jam for a solution.
Tag Archives: logarithm
Logging Problem
This is a delightful little problem from Dick Hess that exercises one’s basic facility with logarithms:
“Define x as 
Find an expression for 
in terms of x where the only constants appearing are integers.”
See the Logging Problem for a solution.
Complex Numbers – Geometric Viewpoint
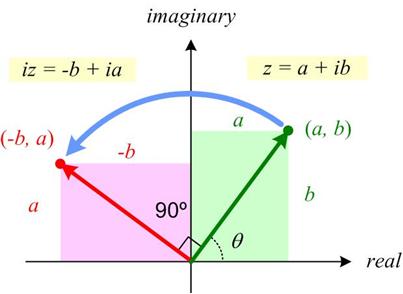This may be a futile attempt at an elementary introduction to complex variables by emphasizing their geometric properties. The elementary part is probably undermined by an initial discussion of field extensions and a necessary reference to trigonometry. Hopefully, the suppression of the explicit use of complex powers of Euler’s constant e until the very end will allow the geometric ideas to have center stage. A primary goal of the essay is to realize that complex polynomials involve sums of circles in the plane. The image of real polynomials as wavy curves in the plane is misleading for an understanding of complex behavior. See Complex Numbers – Geometric Viewpoint.
Mercator Projection Balloon
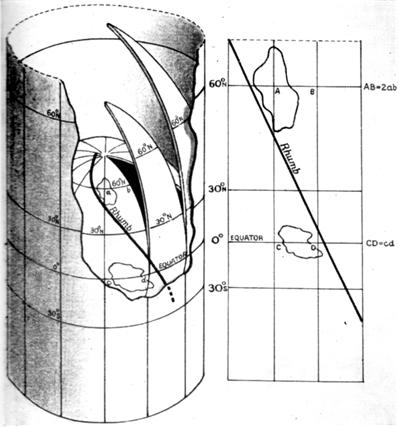Years ago during one of my many excursions into the history of mathematics I wondered how Mercator used logarithms in his map projection (introduced in a 1569 map) when logarithms were not discovered by John Napier (1550-1617) and published in his book Mirifici Logarithmorum Canonis Descriptio until 1614, three years before his death in 1617. The mystery was solved when I read a 1958 book by D. W. Waters which said Edward Wright (1561-1615) in his 1599 book Certaine Errors in Navigation produced his “most important correction, his chart projection, now known as Mercator’s.” Wright did not use logarithms explicitly but rather implicitly through the summing of discrete secants of the latitude as scale factors. But what really caught my attention in the Waters book was this arresting footnote: “Wright explained his projection in terms of a bladder blown up inside a cylinder, a very good analogy.” This article recounts my exploration of this idea. See Mercator Projection Balloon.
(Update 4/2/2022) Balloon Idea as Rubberband
Imagine my surprise when I realized Burkard Polster’s latest Mathologer post “The magic log wheel: How was this missed for 400 years?” involving a circular sliderule presented the logarithm effect as stretching a rubberband around a circle. This is essentially the balloon effect only sort of in reverse.