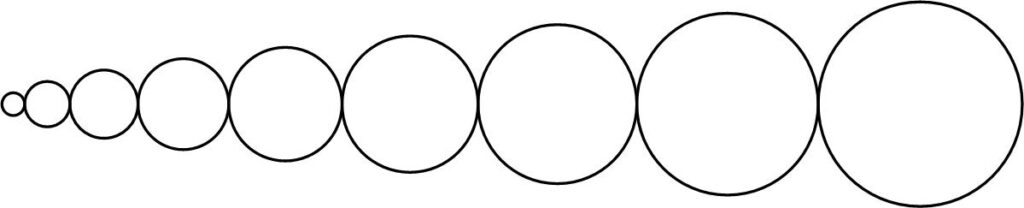
This is a thoughtful little problem from Posamentier’s and Lehmann’s Mathematical Curiosities.
“We have nine wheels touching each other with diameters successively increasing by 1 cm. Beginning with 1 cm as the smallest circle, and 9 cm for the largest circle, how many degrees does the largest circle turn when the smallest circle turns by 90°?”
See the Turning Wheels Puzzle for solutions.
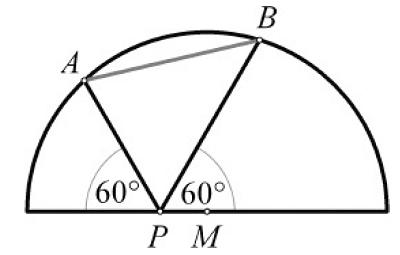This is an interesting problem from Posamentier and Lehmann’s Mathematical Curiosities.
“In the figure we have a semicircle with the point P randomly placed on the diameter. Points A and B are situated on the circle such that they form angles of 60° with the diameter as shown in the figure. This problem asks us to show that the length of AB is equal to the radius of the semicircle.”
See the Ubiquitous Radius Problem
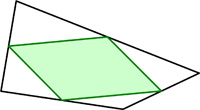I came across this problem in Alfred Posamentier’s book, but I remember I had seen it a couple of places before and had never thought to solve it. At first, it seems like magic.
In any convex quadrilateral (line between any two points in the quadrilateral lies entirely inside the quadrilateral) inscribe a second convex quadrilateral with its vertices on the midpoints of the sides of the first quadrilateral. Show that the inscribed quadrilateral must be a parallelogram.
See the Magic Parallelogram.
(Update 5/15/2020) Continue reading
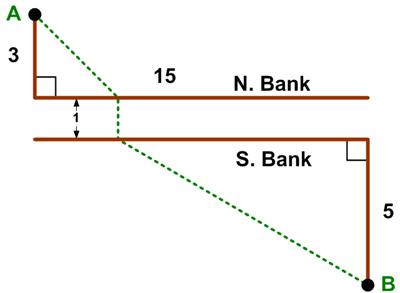This is a riff on a classic problem, given in Challenging Problems in Algebra.
“N. Bank and S. Bank are, respectively, the north and south banks of a river with a uniform width of one mile. Town A is 3 miles north of N. Bank, town B is 5 miles south of S. Bank and 15 miles east of A. If crossing at the river banks is only at right angles to the banks, find the length of the shortest path from A to B.
Challenge. If the rate of land travel is uniformly 8 mph, and the rowing rate on the river is 1 2/3 mph (in still water) with a west to east current of 1 1/3 mph, find the shortest time it takes to go from A to B. [The path across the river must still be perpendicular to the banks.]”
See the River Crossing for a solution.
