Triangle Projection Problem

This is a Maths Item of the Month (MIOM) problem that seems opaque at first.  (“The Maths Item of the Month is a monthly problem aimed at teachers and students of GCSE and A level Mathematics.”)

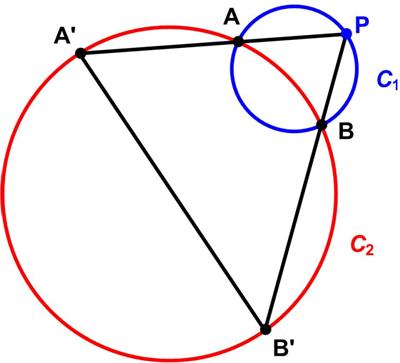
“Two fixed circles, C1 and C2, intersect at A and B.  P is on C1.  PA and PB produced meet C2 at A’ and B’ respectively.  How does the length of the chord A’B’ change as P moves?”

Just start noticing relationships and the answer falls out nicely.

(MIOM problems often appear on MathsMonday and are also produced by Mathematics Education Innovation (MEI).)

Answer.

See the Triangle Projection Problem for a solution.

Post Views: 442

Broken Diagonal Problem

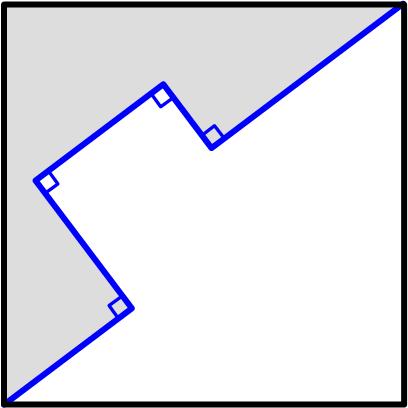This is a nice problem from the UKMT Senior Mathematics Challenge for 2022:

“Five line segments of length 2, 2, 2, 1 and 3 connect two corners of a square as shown in the diagram. What is the shaded area?

A 8____B 9____C 10____D 11____E 12”

The pleasure of solving this problem may be lessened if one is under a time crunch, as is the case with all these timed tests.

Answer.

See the Broken Diagonal Problem for solutions.

Post Views: 87

Road Construction Problem

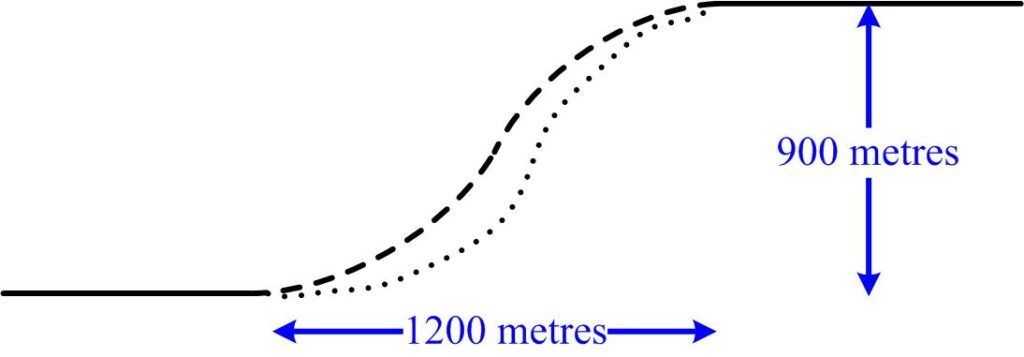This is an interesting problem from the Scottish Mathematics Council (SMC) 2014 Senior  Math Challenge .

“Two straight sections of a road, each running from east to west, and located as shown, are to be joined smoothly by a new roadway consisting of arcs of two circles of equal radius. The existing roads are to be tangents at the joins and the arcs themselves are to have a common tangent where they meet.  Find the length of the radius of these arcs.”

Answer.

See the Road Construction Problem for solutions.

Post Views: 135

Falling Sound Problem

This math problem from Colin Hughes’s Maths Challenge website (mathschallenge.net) hearkens back to basic physics.

“A boy drops a stone down a well and hears the splash from the bottom after three seconds.  Given that sound travels at a constant speed of 300 m/s and the acceleration of the stone due to gravity is 10 m/s2, how deep is the well?”

Answer.

See the Falling Sound Problem for solutions.

Post Views: 3,161

Neuberg’s Theorem

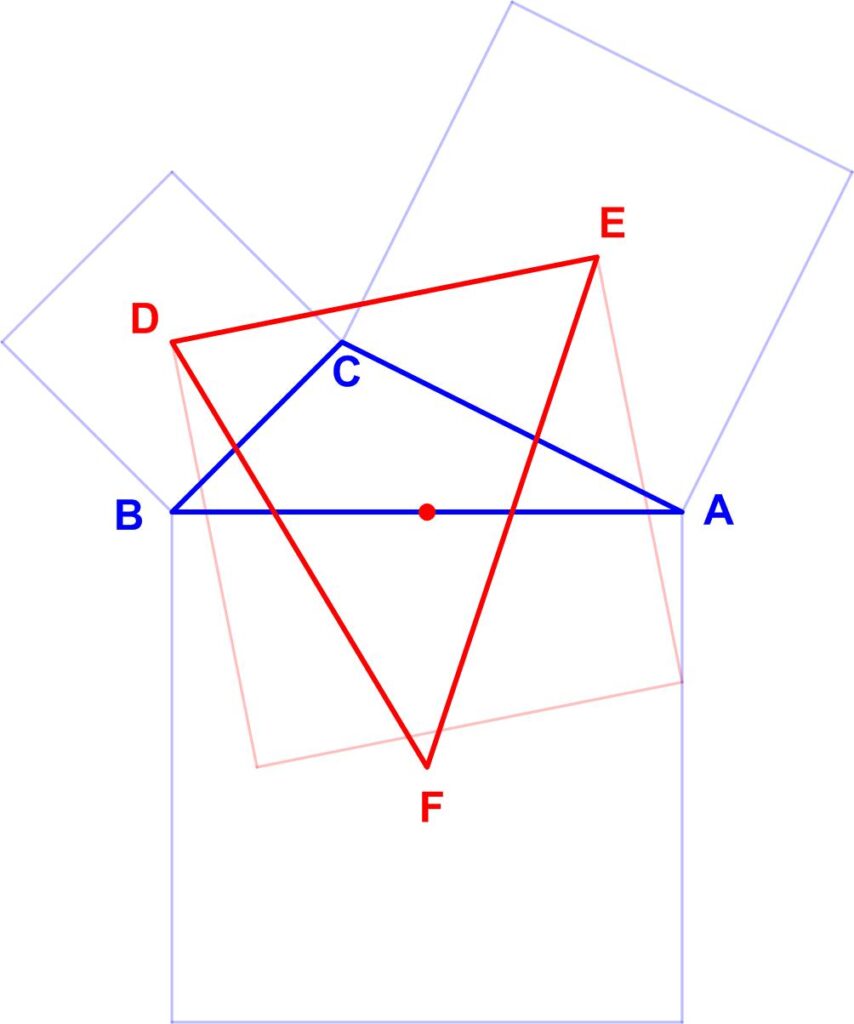This turned out to be a challenging puzzle from the 1980 Canadian Math Society’s magazine, Crux Mathematicorum.

“Proposed by Leon Bankoff, Los Angeles, California.

Professor Euclide Paracelso Bombasto Umbugio has once again retired to his tour d’ivoire where he is now delving into the supersophisticated intricacies of the works of Grassmann, as elucidated by Forder’s Calculus of Extension. His goal is to prove Neuberg’s Theorem:

If D, E, F are the centers of squares described externally on the sides of a triangle ABC, then the midpoints of these sides are the centers of squares described internally on the sides of triangle DEF.  [The accompanying diagram shows only one internally described square.]

Help the dedicated professor emerge from his self-imposed confinement and enjoy the thrill of hyperventilation by showing how to solve his problem using only highschool, synthetic, Euclidean, ‘plain’ geometry.”

Alas, my plane geometry capability was inadequate to solve the puzzle that way, so I had to resort to the sledge hammer of analytic geometry, trigonometry, and complex variables.

See Neuberg’s Theorem

Post Views: 108

Minimum Path Via Circle

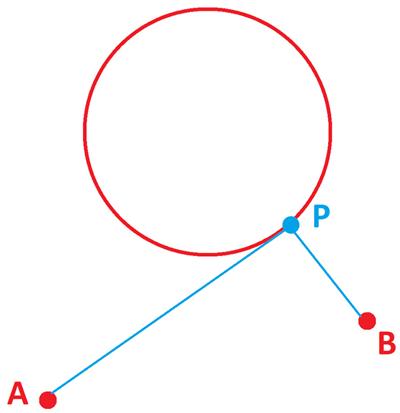James Tanton provides another imaginative problem on Twitter.

“I am at point A and want to walk to point B via some point, any point, P on the circle. What point P should I choose so that my journey A → P → B is as short as possible?”

Hint: I got ideas for a solution from two of my posts, “Square Root Minimum” and “Maximum Product”.

See Minimum Path Via Circle

Post Views: 79

Refabulating Widgets

This is a work problem from Geoffrey Mott-Smith from 1954.

“ ‘If a man can do a job in one day, how long will it take two men to do the job?’

No book of puzzles, I take it, is complete without such a question. I will not blame the reader in the least if he hastily turns the page, for I, too, was annoyed by “If a man” conundrums in my schooldays. Besides, the answer in the back of the book was always wrong. Everybody knows it will take the two men two days to do the job, because they will talk about women and the weather, they will argue about how the job is to be done, they will negotiate as to which is to do it. In schoolbooks the masons and bricklayers are not men, they are robots.

Strictly on the understanding that I am really talking about robots, I will put it to you:

If a tinker and his helper can refabulate a widget in 2 days, and if the tinker working with the apprentice instead would take 3 days, while the helper and the apprentice would take 6 days to do the job, how long would it take each working alone to refabulate the widget?”

Answer.

See Refabulating Widgets for a solution.

Post Views: 80
  1. Pages:
  3. 1
  4. ...
  5. 5
  6. 6
  7. 7
  8. 8
  9. 9
  10. 10
  11. 11
  12. ...
  13. 37